Arithmetik
Die Arithmetik (von griechisch ἀριθμός arithmós, „Zahl“, davon abgeleitet das Adjektiv ἀριθμητικός arithmētikós, „zum Zählen oder Rechnen gehörig“, und τέχνη téchnē, „Kunst“, wörtlich „die zum Zählen oder Rechnen gehörige Kunst“) ist ein Teilgebiet der Mathematik. Sie umfasst das Rechnen mit den Zahlen, vor allem den natürlichen Zahlen. Sie beschäftigt sich mit den Grundrechenarten, also mit der Addition (Zusammenzählen), Subtraktion (Abziehen), Multiplikation (Vervielfachen), Division (Teilen) sowie den zugehörigen Rechengesetzen (mathematische Operatoren bzw. Kalküle). Zur Arithmetik gehört auch die Teilbarkeitslehre mit den Gesetzen der Teilbarkeit ganzer Zahlen sowie der Division mit Rest. Die Arithmetik kann als Teil der Algebra verstanden werden, etwa als „Lehre von den algebraischen Eigenschaften der Zahlen“. Die Arithmetik leitet zur Zahlentheorie über, die sich im weitesten Sinn mit den Eigenschaften der Zahlen beschäftigt. Die Arithmetik ist ein Kalkül. ⓘ

Geschichte
Die Vorgeschichte der Arithmetik beschränkt sich auf einige wenige Artefakte, die auf die Vorstellung von Addition und Subtraktion hindeuten. Das bekannteste ist der Ishango-Knochen aus Zentralafrika, der aus der Zeit zwischen 20.000 und 18.000 v. Chr. stammt, dessen Interpretation jedoch umstritten ist. ⓘ
Aus den frühesten schriftlichen Aufzeichnungen geht hervor, dass die Ägypter und Babylonier bereits 2000 v. Chr. alle elementaren Rechenoperationen verwendeten: Addition, Subtraktion, Multiplikation und Division. Diese Artefakte geben nicht immer Aufschluss über das spezifische Verfahren zur Lösung von Problemen, aber die Merkmale des jeweiligen Zahlensystems beeinflussen die Komplexität der Methoden stark. Das hieroglyphische System der ägyptischen Ziffern stammt ebenso wie die späteren römischen Ziffern von Strichmännchen ab, die zum Zählen verwendet wurden. In beiden Fällen führte dieser Ursprung zu Werten, die eine Dezimalbasis verwendeten, aber keine Positionsschreibweise enthielten. Komplexe Berechnungen mit römischen Ziffern erforderten die Hilfe einer Zähltafel (oder des römischen Abakus), um die Ergebnisse zu erhalten. ⓘ
Frühe Zahlensysteme, die eine Positionsschreibweise enthielten, waren nicht dezimal; dazu gehören das Sexagesimalsystem (Basis 60) für babylonische Zahlen und das Vigesimalsystem (Basis 20), das die Maya-Zahlen definierte. Aufgrund des Stellenwertkonzepts trug die Möglichkeit, dieselben Ziffern für verschiedene Werte wiederzuverwenden, zu einfacheren und effizienteren Rechenmethoden bei. ⓘ
Die kontinuierliche historische Entwicklung der modernen Arithmetik beginnt mit der hellenistischen Periode des antiken Griechenlands; sie entstand viel später als die babylonischen und ägyptischen Beispiele. Vor den Arbeiten von Euklid um 300 v. Chr. überschnitten sich die griechischen Studien zur Mathematik mit philosophischen und mystischen Überzeugungen. Nikomachos ist ein Beispiel für diese Sichtweise, da er in seinem Werk Einführung in die Arithmetik den früheren pythagoreischen Ansatz für Zahlen und ihre Beziehungen zueinander verwendet. ⓘ
Die griechischen Ziffern wurden von Archimedes, Diophantus und anderen in einer Positionsnotation verwendet, die sich nicht sehr von der modernen Notation unterscheidet. Den alten Griechen fehlte bis zur hellenistischen Periode ein Symbol für die Null, und sie verwendeten drei getrennte Sätze von Symbolen als Ziffern: einen Satz für die Einerstelle, einen für die Zehnerstelle und einen für die Hunderterstelle. Für die Tausenderstelle wurden die Symbole der Einerstelle wiederverwendet und so weiter. Ihr Additionsalgorithmus war identisch mit der modernen Methode, und ihr Multiplikationsalgorithmus war nur geringfügig anders. Ihr Algorithmus für die lange Division war derselbe, und der Algorithmus für die ziffernweise Quadratwurzel, der erst im 20. Jahrhundert populär wurde, war Archimedes bekannt (der ihn möglicherweise erfunden hat). Er zog ihn der Hero-Methode der sukzessiven Annäherung vor, weil sich eine einmal berechnete Ziffer nicht mehr ändert und die Quadratwurzeln perfekter Quadrate, wie 7485696, sofort als 2736 enden. Für Zahlen mit einem Bruchteil, wie 546,934, wurden negative Potenzen von 60 verwendet - anstelle von negativen Potenzen von 10 für den Bruchteil 0,934. ⓘ
Die alten Chinesen verfügten über fortgeschrittene arithmetische Studien, die von der Shang-Dynastie bis zur Tang-Dynastie reichten, von den Grundzahlen bis zur fortgeschrittenen Algebra. Die alten Chinesen verwendeten eine Positionsschreibweise, die der der Griechen ähnelte. Da auch ihnen ein Symbol für die Null fehlte, hatten sie einen Satz von Symbolen für die Einerstelle und einen zweiten für die Zehnerstelle. Für die Hunderterstelle wurden dann die Symbole für die Einerstelle wiederverwendet, und so weiter. Ihre Symbole basierten auf den antiken Zählstäben. Der genaue Zeitpunkt, zu dem die Chinesen mit der Positionsdarstellung zu rechnen begannen, ist nicht bekannt, doch weiß man, dass die Einführung vor 400 v. Chr. begann. Die alten Chinesen waren die ersten, die negative Zahlen sinnvoll entdeckten, verstanden und anwendeten. Dies wird in den Neun Kapiteln über die mathematische Kunst (Jiuzhang Suanshu) erläutert, die von Liu Hui aus dem 2. ⓘ
Bei der allmählichen Entwicklung des hindu-arabischen Zahlensystems wurden unabhängig voneinander das Konzept der Stellenwerte und die Positionsnotation entwickelt, die die einfacheren Berechnungsmethoden mit einer Dezimalbasis und der Verwendung einer Ziffer, die für 0 steht, kombinierte. Dies ermöglichte es dem System, sowohl große als auch kleine Zahlen konsistent darzustellen - ein Ansatz, der schließlich alle anderen Systeme ersetzte. Im frühen 6. Jahrhundert n. Chr. nahm der indische Mathematiker Aryabhata eine bestehende Version dieses Systems in seine Arbeit auf und experimentierte mit verschiedenen Notationen. Im 7. Jahrhundert führte Brahmagupta die 0 als eigene Zahl ein und bestimmte die Ergebnisse für Multiplikation, Division, Addition und Subtraktion der Null und aller anderen Zahlen - mit Ausnahme des Ergebnisses der Division durch Null. Sein Zeitgenosse, der syrische Bischof Severus Sebokht (650 n. Chr.), sagte: "Die Inder besitzen eine Rechenmethode, die man mit keinem Wort genug loben kann. Ihr rationales System der Mathematik oder ihre Methode der Berechnung. Ich meine das System mit den neun Symbolen." Auch die Araber lernten diese neue Methode und nannten sie hesab. ⓘ

Obwohl der Codex Vigilanus bereits 976 n. Chr. eine frühe Form der arabischen Ziffern (ohne 0) beschrieb, war Leonardo von Pisa (Fibonacci) nach der Veröffentlichung seines Buches Liber Abaci im Jahr 1202 in erster Linie für die Verbreitung ihrer Verwendung in ganz Europa verantwortlich. Er schrieb: "Die Methode der Inder (lateinisch Modus Indorum) übertrifft jede bekannte Berechnungsmethode. Es ist eine wunderbare Methode. Sie rechnen mit neun Zahlen und dem Symbol Null". ⓘ
Im Mittelalter war die Arithmetik eine der sieben freien Künste, die an den Universitäten gelehrt wurden. ⓘ
Die Blütezeit der Algebra in der mittelalterlichen islamischen Welt und auch im Europa der Renaissance war eine Folge der enormen Vereinfachung des Rechnens durch die Dezimalschreibweise. ⓘ
Es wurden verschiedene Arten von Hilfsmitteln erfunden und weithin verwendet, um numerische Berechnungen zu unterstützen. Vor der Renaissance waren es verschiedene Arten von Abaci. Zu den neueren Beispielen gehören Rechenschieber, Nomogramme und mechanische Rechenmaschinen, wie die Pascalsche Rechenmaschine. Gegenwärtig werden sie von elektronischen Rechenmaschinen und Computern verdrängt. ⓘ
Als Wissenschaft wurde die Arithmetik von den Griechen begründet. Aus der vorgriechischen Zeit sind zum Beispiel von den Ägyptern und den Babyloniern lediglich empirische Regeln zur Lösung von Aufgaben aus dem praktischen Leben überliefert. Für die Pythagoreer machen die natürlichen Zahlen das Wesen der Dinge aus. In den Büchern VII-X von Euklids Elementen werden die damals bekannten arithmetischen/algebraischen/zahlentheoretischen Ergebnisse erstmals zusammenfassend dargestellt. Vor allem nach dem Fall von Toledo (1085) gelangt die von den Arabern gesammelte griechische Mathematik, bereichert um die von den Indern eingeführte Zahl Null und das mit dieser Ergänzung voll entwickelte Dezimalsystem, zurück ins Abendland. In der Renaissance findet eine Wiederbelebung der griechischen Mathematik statt. ⓘ
Auf dieser Basis wird die Arithmetik im 16. und 17. Jahrhundert vor allem durch die Einführung einer zweckmäßigen Zeichensprache für Zahlen und Operationen weiterentwickelt. Damit wird es möglich, Zusammenhänge, die bei verbaler Wiedergabe sehr undurchsichtig wirken, mit einem Blick zu überschauen. François Viète (Vieta, 1540–1603) unterteilt die damals „Logistik“ genannte Rechenkunst in eine logistica numerosa, in unserem Sinne die Arithmetik, und eine logistica speciosa, aus der sich die Algebra entwickelt. Er benutzt für Zahlengrößen Buchstaben und als Operationszeichen + für die Addition, - für die Subtraktion und den Bruchstrich für die Division. William Oughtred (1574–1660) benutzt x als Zeichen der Multiplikation, das er aber auch mal weglässt. Der heute übliche Multiplikationspunkt geht auf Gottfried Wilhelm Leibniz (1646–1716) zurück. John Johnson benutzt seit 1663 den heute üblichen Doppelpunkt (:) für die Division. Thomas Harriot (1560–1621) verwendet die heute üblichen Zeichen für „größer als“ (>) und „kleiner als“ (<) sowie kleine Buchstaben als Variablen für Zahlen. Robert Recorde (1510–1558) führt das Gleichheitszeichen (=) ein. Von René Descartes (1596–1650) stammt die Schreibweise für Quadrate. Leibniz nimmt mit dem Versuch einer axiomatischen Begründung des Rechnens mit natürlichen Zahlen Gedanken der modernen mathematischen Grundlagenforschung vorweg. ⓘ
Carl Friedrich Gauß (1777–1855) wird gerne zitiert mit der Aussage: „Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik.“ – Diese Wortschöpfung lässt die Liebe zur Zahlentheorie bei C. F. Gauß erkennen und zeigt, wie sehr Mathematiker sich dieser Teildisziplin verschreiben können. Wie Gauß selber in der Vorrede seiner berühmten „Untersuchungen über höhere Arithmetik“ (siehe Literatur) bemerkt, gehören die Theorie der Kreisteilung oder der regulären Polygone, welche im siebenten Abschnitt behandelt wird, zwar an und für sich nicht in die Arithmetik; doch müssen ihre Prinzipien einzig und allein aus der höheren Arithmetik geschöpft werden. Da sich die heutige Zahlentheorie weit darüber hinaus entwickelt hat, wird lediglich die elementare Zahlentheorie auch als arithmetische Zahlentheorie (= höhere Arithmetik nach Gauß) bezeichnet. Die Bezeichnung „Arithmetik“ (elementare Arithmetik nach Gauß) im eigentlichen Sinne ist zur Hauptsache dem Rechnen vorbehalten. ⓘ
Leopold Kronecker (1823–1891) wird der Ausspruch zugeschrieben: „Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk.“ ⓘ
Arithmetische Operationen
Die Grundrechenarten sind Addition, Subtraktion, Multiplikation und Division. Die Arithmetik umfasst jedoch auch fortgeschrittenere Operationen wie die Manipulation von Prozentsätzen, Quadratwurzeln, Potenzierung, logarithmischen Funktionen und sogar trigonometrischen Funktionen, ebenso wie die Logarithmen (Prothaphärese). Arithmetische Ausdrücke müssen entsprechend der vorgesehenen Reihenfolge der Operationen ausgewertet werden. Es gibt mehrere Methoden, dies zu spezifizieren, entweder - am häufigsten zusammen mit der Infix-Notation - durch die explizite Verwendung von Klammern und die Anwendung von Präzedenzregeln oder durch die Verwendung einer Präfix- oder Postfix-Notation, die die Reihenfolge der Ausführung eindeutig festlegen. Jede Menge von Objekten, auf denen alle vier arithmetischen Operationen (außer der Division durch Null) ausgeführt werden können und die den üblichen Gesetzen (einschließlich der Distributivität) gehorchen, wird als Feld bezeichnet. ⓘ
Addition
Die Addition, bezeichnet durch das Symbol bezeichnet wird, ist die grundlegendste Operation der Arithmetik. In ihrer einfachen Form verbindet die Addition zwei Zahlen, die Summanden oder Terme, zu einer einzigen Zahl, der Summe der Zahlen (z. B. 2 + 2 = 4 oder 3 + 5 = 8). ⓘ
Die Addition von endlich vielen Zahlen kann als wiederholte einfache Addition betrachtet werden; dieses Verfahren wird als Summation bezeichnet, ein Begriff, der auch für die Definition der "Addition von unendlich vielen Zahlen" in einer unendlichen Reihe verwendet wird. Die wiederholte Addition der Zahl 1 ist die einfachste Form des Zählens; das Ergebnis der Addition von 1 wird gewöhnlich als Nachfolger der ursprünglichen Zahl bezeichnet. ⓘ
Die Addition ist kommutativ und assoziativ, so dass die Reihenfolge, in der endlich viele Terme addiert werden, keine Rolle spielt. ⓘ
Die Zahl 0 hat die Eigenschaft, dass sie, wenn sie zu einer beliebigen Zahl addiert wird, dieselbe Zahl ergibt; sie ist also das Identitätselement der Addition bzw. die additive Identität. ⓘ
Für jede Zahl x gibt es eine Zahl mit der Bezeichnung -x, die als das Gegenteil von x bezeichnet wird, so dass x + (-x) = 0 und (-x) + x = 0 ist. Das Gegenteil von x ist also die Umkehrung von x in Bezug auf die Addition oder die additive Umkehrung von x. Zum Beispiel ist das Gegenteil von 7 -7, da 7 + (-7) = 0. ⓘ
Die Addition kann auch geometrisch interpretiert werden, wie im folgenden Beispiel. Hat man zwei Stäbe der Länge 2 und 5, so ergibt sich, wenn man die Stäbe hintereinander ausrichtet, die Länge des kombinierten Stabes 7, da 2 + 5 = 7 ist. ⓘ
Subtraktion
Die Subtraktion, bezeichnet mit dem Symbol bezeichnet wird, ist die umgekehrte Operation zur Addition. Bei der Subtraktion wird die Differenz zwischen zwei Zahlen ermittelt, also der Minuend minus der Subtrahend: D = M - S. Unter Rückgriff auf die zuvor aufgestellte Addition bedeutet dies, dass die Differenz die Zahl ist, die, wenn sie zum Subtrahenden addiert wird, den Minuend ergibt: D + S = M. ⓘ
Für positive Argumente gilt M und S:
- Wenn der Minuend größer ist als der Subtrahend, ist die Differenz D positiv.
- Ist der Minuend kleiner als der Subtrahend, so ist die Differenz D negativ.
Wenn Minuend und Subtrahend gleich sind, ist die Differenz D in jedem Fall gleich 0. ⓘ
Die Subtraktion ist weder kommutativ noch assoziativ. Aus diesem Grund wird die Konstruktion dieser inversen Operation in der modernen Algebra häufig zugunsten der Einführung des Konzepts der inversen Elemente (wie unter ) verworfen, wobei die Subtraktion als Addition des additiven Kehrwerts des Subtrahenden zum Minuend betrachtet wird, d. h. a - b = a + (-b). Der unmittelbare Preis für den Verzicht auf die binäre Operation der Subtraktion ist die Einführung der (trivialen) unären Operation, die für jede beliebige Zahl die additive Inverse liefert, und der Verlust des unmittelbaren Zugangs zum Begriff der Differenz, der bei negativen Argumenten potenziell irreführend ist. ⓘ
Für jede Darstellung von Zahlen gibt es Methoden zur Berechnung von Ergebnissen, von denen einige besonders vorteilhaft sind, indem sie Verfahren, die für eine Operation existieren, durch kleine Änderungen auch für andere nutzen. Beispielsweise können Digitalrechner vorhandene Additionsschaltungen wiederverwenden und zusätzliche Schaltungen für die Implementierung einer Subtraktion einsparen, indem sie das Zweierkomplementverfahren für die Darstellung der additiven Inversen verwenden, das in der Hardware äußerst einfach zu implementieren ist (Negation). Der Preis dafür ist die Halbierung des Zahlenbereichs bei einer festen Wortlänge. ⓘ
Eine früher weit verbreitete Methode, um bei Kenntnis des fälligen und des gegebenen Betrages zu einem korrekten Wechselgeldbetrag zu kommen, ist das Aufwärtszählen, bei dem der Wert der Differenz nicht explizit erzeugt wird. Angenommen, es wird ein Betrag P gegeben, um den geforderten Betrag Q zu zahlen, wobei P größer als Q ist. Anstatt explizit die Subtraktion P - Q = C durchzuführen und diesen Betrag C als Wechselgeld abzuzählen, wird das Geld beginnend mit dem Nachfolger von Q abgezählt und in den Schritten der Währung fortgesetzt, bis P erreicht ist. Obwohl der abgezählte Betrag dem Ergebnis der Subtraktion P - Q entsprechen muss, wurde die Subtraktion nie wirklich durchgeführt, und der Wert von P - Q wird bei dieser Methode nicht angegeben. ⓘ
Multiplikation
Die Multiplikation, bezeichnet durch die Symbole oder bezeichnet wird, ist die zweite Grundoperation der Arithmetik. Auch bei der Multiplikation werden zwei Zahlen zu einer einzigen Zahl, dem Produkt, zusammengefasst. Die beiden ursprünglichen Zahlen werden als Multiplikator und Multiplikand bezeichnet, meist werden beide einfach Faktoren genannt. ⓘ
Die Multiplikation kann als eine Skalierungsoperation betrachtet werden. Stellt man sich die Zahlen auf einer Linie liegend vor, so ist die Multiplikation mit einer Zahl größer als 1, z. B. x, gleichbedeutend mit einer gleichmäßigen Streckung aller Zahlen von 0 weg, so dass die Zahl 1 selbst an die Stelle von x gestreckt wird. In ähnlicher Weise kann man sich die Multiplikation mit einer Zahl kleiner als 1 als Quetschung gegen 0 vorstellen, und zwar so, dass die Zahl 1 zum Multiplikanden kommt. ⓘ
Eine andere Sichtweise auf die Multiplikation ganzer Zahlen (die auf rationale Zahlen ausgedehnt werden kann, aber für reelle Zahlen nicht sehr zugänglich ist) besteht darin, sie als wiederholte Addition zu betrachten. Zum Beispiel. 3 × 4 entspricht entweder der Addition von 3 mal 4 oder 4 mal 3, was das gleiche Ergebnis ergibt. Es gibt unterschiedliche Meinungen über den Nutzen dieser Paradigmen für den Mathematikunterricht. ⓘ
Die Multiplikation ist kommutativ und assoziativ; außerdem ist sie distributiv gegenüber Addition und Subtraktion. Die multiplikative Identität ist 1, da die Multiplikation einer beliebigen Zahl mit 1 dieselbe Zahl ergibt. Der multiplikative Kehrwert für jede Zahl außer 0 ist der Kehrwert dieser Zahl, da die Multiplikation des Kehrwerts einer beliebigen Zahl mit der Zahl selbst die multiplikative Identität 1 ergibt. 0 ist die einzige Zahl ohne multiplikativen Kehrwert, und das Ergebnis der Multiplikation einer beliebigen Zahl mit 0 ist wiederum 0. Man sagt, dass 0 nicht in der multiplikativen Gruppe der Zahlen enthalten ist. ⓘ
Das Produkt von a und b wird als a × b oder a-b geschrieben. Wenn a oder b Ausdrücke sind, die nicht einfach mit Ziffern geschrieben werden, schreibt man sie auch durch einfache Aneinanderreihung: ab. In Programmiersprachen und Softwarepaketen (in denen man nur Zeichen verwenden kann, die normalerweise auf einer Tastatur zu finden sind), wird es oft mit einem Sternchen geschrieben: a * b. ⓘ
Die Algorithmen, die die Multiplikation für die verschiedenen Zahlendarstellungen implementieren, sind bei weitem aufwendiger und kostspieliger als die für die Addition. Diejenigen, die für die manuelle Berechnung zugänglich sind, beruhen entweder auf der Zerlegung der Faktoren in einzelne Stellenwerte und der Anwendung der wiederholten Addition oder auf der Verwendung von Tabellen oder Rechenschiebern, wodurch die Multiplikation auf die Addition und umgekehrt abgebildet wird. Diese Methoden sind veraltet und werden nach und nach durch mobile Geräte ersetzt. Computer verwenden verschiedene ausgeklügelte und hoch optimierte Algorithmen, um Multiplikation und Division für die verschiedenen von ihrem System unterstützten Zahlenformate durchzuführen. ⓘ
Division
Die Division, bezeichnet durch die Symbole oder bezeichnet, ist im Wesentlichen die umgekehrte Operation zur Multiplikation. Bei der Division wird der Quotient aus zwei Zahlen ermittelt, der Dividend geteilt durch den Divisor. Nach den üblichen Regeln ist der Dividenden durch Null geteilt undefiniert. Für eindeutige positive Zahlen gilt: Ist der Dividend größer als der Divisor, ist der Quotient größer als 1, andernfalls ist er kleiner oder gleich 1 (eine ähnliche Regel gilt für negative Zahlen). Der Quotient multipliziert mit dem Divisor ergibt immer die Dividende. ⓘ
Die Division ist weder kommutativ noch assoziativ. Daher wird, wie in erläutert, die Konstruktion der Division in der modernen Algebra zugunsten der Konstruktion der Umkehrelemente in Bezug auf die Multiplikation, wie in eingeführt, verworfen. Die Division ist also die Multiplikation des Dividenden mit dem Kehrwert des Divisors als Faktoren, d. h. a ÷ b = a ×. ⓘ
Innerhalb der natürlichen Zahlen gibt es auch einen anderen, aber verwandten Begriff, die euklidische Division, die nach der "Division" eines natürlichen N (Zähler) durch einen natürlichen D (Nenner) zwei Zahlen ausgibt: erstens ein natürliches Q (Quotient) und zweitens ein natürliches R (Rest), so dass N = D×Q + R und 0 ≤ R < Q. ⓘ
In einigen Kontexten, darunter Computerprogrammierung und fortgeschrittene Arithmetik, wird die Division um einen weiteren Ausgang für den Rest erweitert. Dies wird oft als separate Operation behandelt, die Modulo-Operation, bezeichnet durch das Symbol oder das Wort bezeichnet, manchmal aber auch als zweiter Ausgang für eine "divmod"-Operation. In jedem Fall hat die modulare Arithmetik eine Vielzahl von Anwendungsfällen. Verschiedene Implementierungen der Division (bodenständig, abgeschnitten, euklidisch usw.) entsprechen verschiedenen Implementierungen des Modulos. ⓘ
Grundlegender Satz der Arithmetik
Der Fundamentalsatz der Arithmetik besagt, dass jede ganze Zahl größer als 1 eine eindeutige Primfaktorzerlegung hat (eine Darstellung einer Zahl als Produkt von Primfaktoren), wobei die Reihenfolge der Faktoren nicht berücksichtigt wird. Zum Beispiel hat 252 nur eine Primfaktorzerlegung:
- 252 = 22 × 32 × 71 ⓘ
In Euklids Elemente wurde dieser Satz zum ersten Mal aufgestellt und teilweise bewiesen (er wird als Euklids Lemma bezeichnet). Der Fundamentalsatz der Arithmetik wurde erstmals von Carl Friedrich Gauß bewiesen. ⓘ
Der Fundamentalsatz der Arithmetik ist einer der Gründe, warum 1 nicht als Primzahl gilt. Weitere Gründe sind das Sieb des Eratosthenes und die Definition einer Primzahl selbst (eine natürliche Zahl größer als 1, die nicht durch Multiplikation zweier kleinerer natürlicher Zahlen gebildet werden kann). ⓘ
Dezimale Arithmetik
Die Dezimaldarstellung bezieht sich im allgemeinen Sprachgebrauch ausschließlich auf das schriftliche Zahlensystem, das arabische Ziffern als Ziffern für eine Positionsnotation mit der Radix 10 ("Dezimal") verwendet; jedes auf Potenzen von 10 basierende Zahlensystem, z. B. griechische, kyrillische, römische oder chinesische Ziffern, kann jedoch konzeptionell als "Dezimalnotation" oder "Dezimaldarstellung" bezeichnet werden. ⓘ
Die modernen Methoden für die vier Grundrechenarten (Addition, Subtraktion, Multiplikation und Division) wurden erstmals von Brahmagupta aus Indien entwickelt. Diese Methode war im mittelalterlichen Europa als "Modus Indorum" oder Methode der Inder bekannt. Die Positionsnotation (auch "Stellenwertnotation" genannt) bezieht sich auf die Darstellung oder Kodierung von Zahlen unter Verwendung desselben Symbols für die verschiedenen Größenordnungen (z. B. "Einerstelle", "Zehnerstelle", "Hunderterstelle") und, mit einem Radixpunkt, unter Verwendung derselben Symbole zur Darstellung von Brüchen (z. B. "Zehntelstelle", "Hunderterstelle"). Zum Beispiel bedeutet 507,36 5 Hunderter (102), plus 0 Zehner (101), plus 7 Einer (100), plus 3 Zehntel (10-1) plus 6 Hundertstel (10-2). ⓘ
Das Konzept der 0 als eine mit den anderen Grundziffern vergleichbare Zahl ist für diese Notation von wesentlicher Bedeutung, ebenso wie die Verwendung der 0 als Platzhalter und die Definition der Multiplikation und Addition mit 0. Die Verwendung der 0 als Platzhalter und damit die Verwendung einer Positionsnotation ist erstmals in dem indischen Jain-Text Lokavibhâga aus dem Jahr 458 n. Chr. bezeugt, und erst im frühen 13. Jahrhundert wurden diese Konzepte, die durch die Gelehrsamkeit der arabischen Welt übermittelt wurden, von Fibonacci unter Verwendung des hindu-arabischen Zahlensystems in Europa eingeführt. ⓘ
Die Algorithmik umfasst alle Regeln für die Durchführung arithmetischer Berechnungen unter Verwendung dieser Art von geschriebenen Ziffern. Zum Beispiel ergibt die Addition die Summe zweier beliebiger Zahlen. Das Ergebnis wird durch die wiederholte Addition einzelner Ziffern von jeder Zahl, die dieselbe Position einnimmt, von rechts nach links berechnet. Eine Additionstabelle mit zehn Zeilen und zehn Spalten zeigt alle möglichen Werte für jede Summe an. Wenn eine einzelne Summe den Wert 9 überschreitet, wird das Ergebnis mit zwei Ziffern dargestellt. Die äußerste rechte Ziffer ist der Wert für die aktuelle Position, und das Ergebnis für die nachfolgende Addition der Ziffern links davon erhöht sich um den Wert der zweiten (äußersten linken) Ziffer, die immer eins (wenn nicht null) ist. Diese Anpassung wird als Übertrag des Wertes 1 bezeichnet. ⓘ
Das Verfahren zur Multiplikation zweier beliebiger Zahlen ist ähnlich wie das Verfahren zur Addition. Eine Multiplikationstabelle mit zehn Zeilen und zehn Spalten listet die Ergebnisse für jedes Ziffernpaar auf. Wenn ein einzelnes Produkt eines Ziffernpaares den Wert 9 überschreitet, erhöht der Übertrag das Ergebnis jeder nachfolgenden Multiplikation von Ziffern links um einen Wert, der der zweiten (ganz linken) Ziffer entspricht, also einem beliebigen Wert zwischen 1 und 8 (9 × 9 = 81). Weitere Schritte bestimmen das Endergebnis. ⓘ
Ähnliche Verfahren gibt es für Subtraktion und Division. ⓘ
Die Erstellung eines korrekten Verfahrens für die Multiplikation hängt von der Beziehung zwischen den Werten benachbarter Ziffern ab. Der Wert einer einzelnen Ziffer in einer Zahl hängt von ihrer Position ab. Außerdem stellt jede Stelle auf der linken Seite einen zehnmal größeren Wert dar als die Stelle auf der rechten Seite. Mathematisch ausgedrückt, erhöht sich der Exponent für die Basis 10 um 1 (nach links) oder verringert sich um 1 (nach rechts). Daher wird der Wert für eine beliebige Ziffer mit einem Wert der Form 10n mit der ganzen Zahl n multipliziert. Die Liste der Werte, die allen möglichen Positionen für eine einzelne Ziffer entsprechen, wird geschrieben als {..., 102, 10, 1, 10-1, 10-2, ...}. ⓘ
Die wiederholte Multiplikation eines beliebigen Wertes in dieser Liste mit 10 ergibt einen anderen Wert in der Liste. In der mathematischen Terminologie wird diese Eigenschaft als Abschluss definiert, und die vorherige Liste wird beschrieben als geschlossen unter Multiplikation. Sie ist die Grundlage für die korrekte Ermittlung der Ergebnisse der Multiplikation mit der vorherigen Technik. Dieses Ergebnis ist ein Beispiel für die Anwendung der Zahlentheorie. ⓘ
Arithmetik mit zusammengesetzten Einheiten
Die Arithmetik mit zusammengesetzten Einheiten ist die Anwendung arithmetischer Operationen auf gemischte Radix-Mengen wie Fuß und Zoll, Gallonen und Pints, Pfund, Shilling und Pence usw. Vor der Einführung des Dezimalsystems für Geld und Maßeinheiten war die Arithmetik mit zusammengesetzten Einheiten in Handel und Industrie weit verbreitet. ⓘ
Grundlegende arithmetische Operationen
Die Techniken, die in der Arithmetik mit zusammengesetzten Einheiten verwendet werden, wurden über viele Jahrhunderte hinweg entwickelt und sind in vielen Lehrbüchern in vielen verschiedenen Sprachen gut dokumentiert. Zusätzlich zu den grundlegenden arithmetischen Funktionen, die in der Dezimalarithmetik vorkommen, werden in der Arithmetik mit zusammengesetzten Einheiten drei weitere Funktionen verwendet:
- ReduktionReduktion, bei der eine zusammengesetzte Menge auf eine einzige Menge reduziert wird, z. B. die Umrechnung einer in Yards, Fuß und Zoll ausgedrückten Entfernung in eine in Zoll ausgedrückte Entfernung.
- Erweiterungist die umgekehrte Funktion zur Reduktion, d. h. die Umrechnung einer Menge, die in einer einzelnen Maßeinheit ausgedrückt ist, in eine zusammengesetzte Einheit, z. B. die Umrechnung von 24 oz in 1 lb 8 oz.
- Normalisierung ist die Umrechnung einer Menge zusammengesetzter Einheiten in eine Standardform, z. B. die Umschreibung von "1 ft 13 in" in "2 ft 1 in". ⓘ
Die Kenntnis der Beziehung zwischen den verschiedenen Maßeinheiten, ihren Vielfachen und Untervielfachen ist ein wesentlicher Bestandteil der Arithmetik mit zusammengesetzten Einheiten. ⓘ
Grundsätze der Arithmetik mit zusammengesetzten Einheiten
Es gibt zwei grundlegende Ansätze für die Arithmetik mit zusammengesetzten Einheiten:
- Reduktions-Expansions-Methode Bei dieser Methode werden alle Variablen mit zusammengesetzten Einheiten auf Variablen mit einer Einheit reduziert, die Berechnung durchgeführt und das Ergebnis wieder in zusammengesetzte Einheiten expandiert. Dieser Ansatz ist für automatisierte Berechnungen geeignet. Ein typisches Beispiel ist die Behandlung der Zeit in Microsoft Excel, wo alle Zeitintervalle intern als Tage und Dezimalbruchteile eines Tages verarbeitet werden.
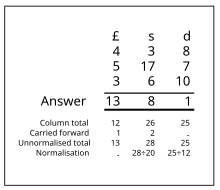
- Fortlaufende Normalisierungsmethode Bei dieser Methode wird jede Einheit separat behandelt und das Problem wird im Laufe der Lösung kontinuierlich normalisiert. Dieser Ansatz, der in klassischen Texten häufig beschrieben wird, eignet sich am besten für manuelle Berechnungen. Ein Beispiel für die fortlaufende Normalisierungsmethode, wie sie bei der Addition angewendet wird, ist unten dargestellt. ⓘ
Die Addition wird von rechts nach links durchgeführt; in diesem Fall werden zuerst Pence, dann Shillings und schließlich Pfund verarbeitet. Die Zahlen unterhalb der "Antwortzeile" sind Zwischenergebnisse. ⓘ
Die Summe in der Pence-Spalte ist 25. Da ein Shilling 12 Pfennige enthält, wird 25 durch 12 geteilt und ergibt 2 mit einem Rest von 1. Der Wert "1" wird dann in die Antwortzeile geschrieben und der Wert "2" in die Shillings-Spalte übertragen. Dieser Vorgang wird mit den Werten in der Schillingsspalte wiederholt, wobei zusätzlich der übertragene Wert aus der Pfennigspalte hinzugefügt wird. Die Zwischensumme wird durch 20 geteilt, da ein Pfund 20 Shillings enthält. Anschließend wird die Pfund-Spalte bearbeitet, aber da das Pfund die größte betrachtete Einheit ist, werden keine Werte aus der Pfund-Spalte übertragen. ⓘ
Der Einfachheit halber wurden im gewählten Beispiel keine Farthings verwendet. ⓘ
Operationen in der Praxis

Im 19. und 20. Jahrhundert wurden verschiedene Hilfsmittel entwickelt, um den Umgang mit zusammengesetzten Einheiten zu erleichtern, insbesondere im Handel. Die gebräuchlichsten Hilfsmittel waren mechanische Kassen, die in Ländern wie dem Vereinigten Königreich so angepasst wurden, dass sie Pfund, Shilling, Pennies und Farthings aufnehmen konnten, sowie "ready reckoners", Bücher für Händler, in denen die Ergebnisse verschiedener Routineberechnungen wie Prozentsätze oder Vielfache verschiedener Geldbeträge katalogisiert wurden. Ein typisches Büchlein, das 150 Seiten umfasste, listete Vielfache "von eins bis zehntausend zu den verschiedenen Preisen von einem Farthing bis zu einem Pfund" auf. ⓘ
Die Schwerfälligkeit der Arithmetik mit zusammengesetzten Einheiten ist seit vielen Jahren bekannt - 1586 veröffentlichte der flämische Mathematiker Simon Stevin eine kleine Broschüre mit dem Titel De Thiende ("der Zehnte"), in der er die allgemeine Einführung des Dezimalsystems für Münzen, Maße und Gewichte für nur eine Frage der Zeit erklärte. In der heutigen Zeit zeigen viele Umrechnungsprogramme, wie z. B. das im Rechner des Betriebssystems Microsoft Windows 7 enthaltene Programm, zusammengesetzte Einheiten in einem reduzierten Dezimalformat an, anstatt ein erweitertes Format zu verwenden (z. B. wird "2,5 ft" statt "2 ft 6 in" angezeigt). ⓘ
Zahlentheorie
Bis zum 19. Jahrhundert war die Zahlentheorie ein Synonym für "Arithmetik". Die behandelten Probleme standen in direktem Zusammenhang mit den Grundrechenarten und betrafen die Primzahl, die Teilbarkeit und die Lösung von Gleichungen mit ganzen Zahlen, wie z. B. Fermats letzter Satz. Es stellte sich heraus, dass die meisten dieser Probleme, obwohl sie sehr elementar sind, sehr schwierig sind und nicht ohne sehr tiefgehende Mathematik gelöst werden können, die Konzepte und Methoden aus vielen anderen Bereichen der Mathematik einbezieht. Dies führte zu neuen Zweigen der Zahlentheorie wie der analytischen Zahlentheorie, der algebraischen Zahlentheorie, der diophantischen Geometrie und der arithmetisch algebraischen Geometrie. Wiles' Beweis von Fermats letztem Satz ist ein typisches Beispiel für die Notwendigkeit anspruchsvoller Methoden, die weit über die klassischen Methoden der Arithmetik hinausgehen, um Probleme zu lösen, die in der elementaren Arithmetik angegeben werden können. ⓘ
Arithmetik im Unterricht
Im Mathematikunterricht der Grundschule liegt der Schwerpunkt häufig auf Algorithmen für die Arithmetik der natürlichen Zahlen, der ganzen Zahlen, der Brüche und der Dezimalzahlen (unter Verwendung des dezimalen Stellenwertsystems). Dieses Studium wird manchmal als Algorismus bezeichnet. ⓘ
Die Schwierigkeit und das unmotivierte Auftreten dieser Algorithmen hat Pädagogen lange Zeit dazu veranlasst, diesen Lehrplan in Frage zu stellen und sich für eine frühzeitige Vermittlung zentraler und intuitiver mathematischer Ideen einzusetzen. Eine bemerkenswerte Bewegung in diese Richtung war die Neue Mathematik der 1960er und 1970er Jahre, die versuchte, die Arithmetik im Sinne einer axiomatischen Entwicklung aus der Mengenlehre zu lehren, ein Echo des vorherrschenden Trends in der höheren Mathematik. ⓘ
Außerdem wurde die Arithmetik von islamischen Gelehrten verwendet, um die Anwendung der Vorschriften zu Zakat und Irth zu lehren. Dies geschah in einem Buch mit dem Titel Das Beste der Arithmetik von Abd-al-Fattah-al-Dumyati. ⓘ
Das Buch beginnt mit den Grundlagen der Mathematik und geht in den späteren Kapiteln zu ihrer Anwendung über. ⓘ