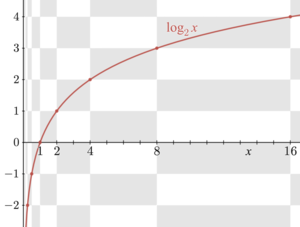
Logarithmus

| Arithmetische Operationen | ||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
In der Mathematik ist der Logarithmus die Umkehrfunktion zur Potenzierung. Das bedeutet, dass der Logarithmus einer gegebenen Zahl x der Exponent ist, auf den eine andere feste Zahl, die Basis b, erhöht werden muss, um diese Zahl x zu erhalten. Im einfachsten Fall zählt der Logarithmus die Anzahl der Vorkommen desselben Faktors bei wiederholter Multiplikation; da z. B. 1000 = 10 × 10 × 10 = 103 ist, ist der "Logarithmus zur Basis 10" von 1000 gleich 3, oder log10 (1000) = 3. Der Logarithmus von x zur Basis b wird als logb (x) bezeichnet, oder ohne Klammern, logb x, oder sogar ohne die explizite Basis, log x, wenn keine Verwechslung möglich ist oder wenn die Basis keine Rolle spielt, wie z. B. in der Big-O-Notation. ⓘ
Der Logarithmus zur Basis 10 (d. h. b = 10) wird als dezimaler oder gewöhnlicher Logarithmus bezeichnet und wird häufig in Wissenschaft und Technik verwendet. Der natürliche Logarithmus hat die Zahl e (d. h. b ≈ 2,718) als Basis; seine Verwendung ist in der Mathematik und Physik weit verbreitet, da das Integral und die Ableitung einfacher sind. Der binäre Logarithmus hat die Basis 2 (d. h. b = 2) und wird häufig in der Computerwissenschaft verwendet. ⓘ
Logarithmen wurden 1614 von John Napier als Mittel zur Vereinfachung von Berechnungen eingeführt. Sie wurden schnell von Navigatoren, Wissenschaftlern, Ingenieuren, Vermessungsingenieuren und anderen übernommen, um hochpräzise Berechnungen einfacher durchführen zu können. Mit Hilfe von Logarithmentabellen können mühsame mehrstellige Multiplikationsschritte durch Nachschlagen in Tabellen und einfachere Additionen ersetzt werden. Dies ist möglich, weil der Logarithmus eines Produkts die Summe der Logarithmen der Faktoren ist:
Vorausgesetzt, b, x und y sind alle positiv und b ≠ 1. Der Rechenschieber, der ebenfalls auf Logarithmen basiert, ermöglicht schnelle Berechnungen ohne Tabellen, allerdings mit geringerer Genauigkeit. Der heutige Begriff des Logarithmus geht auf Leonhard Euler zurück, der ihn im 18. Jahrhundert mit der Exponentialfunktion verband und auch den Buchstaben e als Basis des natürlichen Logarithmus einführte. ⓘ
Logarithmische Skalen reduzieren weitreichende Größen auf kleinere Bereiche. So ist beispielsweise das Dezibel (dB) eine Einheit, die verwendet wird, um Verhältnisse als Logarithmus auszudrücken, vor allem für Signalleistung und Amplitude (wofür der Schalldruck ein gängiges Beispiel ist). In der Chemie ist der pH-Wert ein logarithmisches Maß für den Säuregrad einer wässrigen Lösung. Logarithmen sind in wissenschaftlichen Formeln und bei der Messung der Komplexität von Algorithmen und geometrischen Objekten, so genannten Fraktalen, weit verbreitet. Sie helfen bei der Beschreibung von Häufigkeitsverhältnissen musikalischer Intervalle, tauchen in Formeln zur Zählung von Primzahlen oder zur Annäherung an Faktorzahlen auf, dienen als Grundlage für einige Modelle in der Psychophysik und können bei der forensischen Buchführung helfen. ⓘ
Das Konzept des Logarithmus als Umkehrung der Potenzierung erstreckt sich auch auf andere mathematische Strukturen. Im Allgemeinen ist der Logarithmus jedoch eher eine mehrwertige Funktion. So ist beispielsweise der komplexe Logarithmus die mehrwertige Umkehrung der komplexen Exponentialfunktion. In ähnlicher Weise ist der diskrete Logarithmus die mehrwertige Umkehrung der Exponentialfunktion in endlichen Gruppen; er wird in der Kryptographie mit öffentlichen Schlüsseln verwendet. ⓘ


Mit Logarithmen lassen sich sehr stark wachsende Zahlenreihen übersichtlich darstellen, da der Logarithmus für große Zahlen viel langsamer steigt als die Zahlen selbst. Wie die Gleichung zeigt, kann man durch Logarithmieren eine Multiplikation durch die viel weniger rechenintensive Addition ersetzen. Auch beschreiben Logarithmen auf mathematisch elegante Weise viele technische Prozesse sowie Phänomene der Natur wie etwa das Verhalten einer Halbleiter-Diode, die Spirale eines Schneckenhauses oder die Wahrnehmung unterschiedlicher Lautstärken durch das menschliche Ohr. ⓘ
Begründung
Addition, Multiplikation und Potenzierung sind drei der grundlegendsten arithmetischen Operationen. Der Kehrwert der Addition ist die Subtraktion, und der Kehrwert der Multiplikation ist die Division. Ebenso ist der Logarithmus die umgekehrte Operation der Potenzierung. Bei der Potenzierung wird eine Zahl b, die Basis, auf eine bestimmte Potenz y, den Exponenten, gehoben, um einen Wert x zu erhalten; dies wird als
Zum Beispiel ergibt die Potenzierung von 2 mit 3 den Wert 8: ⓘ
Der Logarithmus zur Basis b ist die umgekehrte Operation, die aus der Eingabe x die Ausgabe y liefert, d. h, ist äquivalent zu wenn b eine positive reelle Zahl ist. (Wenn b keine positive reelle Zahl ist, können sowohl die Potenzierung als auch der Logarithmus definiert werden, können aber mehrere Werte annehmen, was die Definitionen wesentlich komplizierter macht). ⓘ
Einer der wichtigsten historischen Beweggründe für die Einführung von Logarithmen ist die Formel
die es (vor der Erfindung des Computers) ermöglichte, die Berechnung von Multiplikationen und Divisionen auf Additionen, Subtraktionen und Logarithmentabellen zu reduzieren. ⓘ
Definition
Die Logarithmusfunktionen sind die nicht-trivialen, stetigen Lösungen der Funktionalgleichung
Ihre Lösungen erfüllen stets und erweisen sich sogar als differenzierbar. Den natürlichen Logarithmus erhält man dann zusammen mit der Zusatzbedingung
Die Zusatzbedingung ist einer der Gründe dafür, den so erhaltenen Logarithmus als natürlich zu bezeichnen. Wollte man den Logarithmus zu einer anderen Basis über die Zusatzbedingung erhalten, dann müsste man
fordern und würde wieder den natürlichen Logarithmus benötigen. ⓘ
Die triviale Lösung obiger Funktionalgleichung ist die Nullfunktion , die nicht als Logarithmusfunktion angesehen wird, und die einzige Lösung der Funktionalgleichung, für die auch definiert ist. ⓘ
Der Logarithmus vermittelt aufgrund obiger Funktionalgleichung daher insbesondere eine strukturerhaltende Abbildung von den positiven reellen Zahlen mit ihrer multiplikativen Struktur auf die gesamten reellen Zahlen mit deren additiver Struktur. Dies kann man auch explizit als Bedingung fordern und gelangt damit zur Herleitung. ⓘ
Eine äquivalente und prägnantere Definition lautet, dass die Funktion logb die Umkehrfunktion der Funktion . ⓘ
Der Logarithmus kann mathematisch stets als eine Schar von Funktionen (deren Parameter mit bezeichnet sei) von aufgefasst werden. Ihre einzelnen Logarithmusfunktionen sind dabei nur unterschiedliche (reelle, aber ungleich null) Vielfache voneinander. ⓘ
Über den positiven reellen Zahlen kann er auf verschiedene Arten eingeführt werden. Je nach Hintergrund und Intention wird man den einen oder anderen didaktischen Zugang wählen. Die verschiedenen Definitionen des reellen Logarithmus sind dabei untereinander äquivalent und erfolgen hier mit besonderem Fokus auf den natürlichen Logarithmus, der aus Sicht des Mathematikers auf natürliche Weise auftritt, wie bei dem Zugang über die Stammfunktion von erkennbar ist. ⓘ
Beispiele
- log2 16 = 4, da 24 = 2 × 2 × 2 × 2 = 16.
- Logarithmen können auch negativ sein: Da
- log10 150 ist ungefähr 2,176, was zwischen 2 und 3 liegt, so wie 150 zwischen 102 = 100 und 103 = 1000 liegt.
- Für jede Basis b ist logb b = 1 und logb 1 = 0, da b1 = b bzw. b0 = 1 ist. ⓘ
Als Isomorphismus
Die reellwertigen Logarithmen sind genau die stetigen Isomorphismen
- .
Diese Definition legt die Funktion bis auf eine multiplikative Konstante eindeutig fest. ⓘ
Der algebraische Zugang betont ebenso wie der Zugang über die Funktionalgleichung die historische Bedeutung des Logarithmus als Rechenhilfe: Er ermöglicht es, eine Multiplikation in eine Addition „umzuwandeln“. ⓘ
Logarithmische Identitäten
Mehrere wichtige Formeln, die manchmal als logarithmische Identitäten oder logarithmische Gesetze bezeichnet werden, setzen Logarithmen zueinander in Beziehung. ⓘ
Produkt, Quotient, Potenz und Wurzel
Der Logarithmus eines Produkts ist die Summe der Logarithmen der zu multiplizierenden Zahlen; der Logarithmus des Verhältnisses zweier Zahlen ist die Differenz der Logarithmen. Der Logarithmus der p-ten Potenz einer Zahl ist das p-fache des Logarithmus der Zahl selbst; der Logarithmus einer p-ten Wurzel ist der Logarithmus der Zahl geteilt durch p. In der folgenden Tabelle sind diese Identitäten mit Beispielen aufgeführt. Jede der Identitäten lässt sich durch Substitution der Logarithmusdefinitionen ableiten oder in den linken Seiten abgeleitet werden. ⓘ
| Formel | Beispiel ⓘ | |
|---|---|---|
| Produkt | ||
| Quotient | ||
| Potenz | ||
| Wurzel |
Wechsel der Basis
Der Logarithmus logb x lässt sich aus den Logarithmen von x und b in Bezug auf eine beliebige Basis k mit der folgenden Formel berechnen:
Herleitung des Umrechnungsfaktors zwischen Logarithmen beliebiger Basis ⓘ
|
|---|
|
Ausgehend von der definierenden Identität können wir logk auf beide Seiten dieser Gleichung anwenden, um Folgendes zu erhalten
Das Lösen für ergibt:
Angabe des Umrechnungsfaktors von gegebenen -Werten in ihre entsprechenden -Werte zu sein |
Typische wissenschaftliche Rechner berechnen die Logarithmen zu den Basen 10 und e. Logarithmen zu jeder Basis b können mit einem dieser beiden Logarithmen durch die vorstehende Formel bestimmt werden:
Gegeben eine Zahl x und ihr Logarithmus y = logb x zu einer unbekannten Basis b, ist die Basis gegeben durch:
Das ergibt sich aus der Definitionsgleichung zur Potenz von ⓘ
Besondere Basen

Unter allen Basenwahlen sind drei besonders häufig. Diese sind b = 10, b = e (die irrationale mathematische Konstante ≈ 2,71828) und b = 2 (der binäre Logarithmus). In der mathematischen Analyse ist der Logarithmus zur Basis e aufgrund der unten erläuterten analytischen Eigenschaften weit verbreitet. Andererseits sind Logarithmen zur Basis 10 für manuelle Berechnungen im dezimalen Zahlensystem einfach zu verwenden:
So steht log10 (x) in Beziehung zur Anzahl der Dezimalstellen einer positiven ganzen Zahl x: Die Anzahl der Stellen ist die kleinste ganze Zahl, die streng größer ist als log10 (x). Zum Beispiel ist log10(1430) ungefähr 3,15. Die nächste ganze Zahl ist 4, das ist die Anzahl der Stellen von 1430. Sowohl der natürliche Logarithmus als auch der Logarithmus zur Basis 2 werden in der Informationstheorie verwendet, was der Verwendung von nats bzw. Bits als Grundeinheiten der Information entspricht. Binäre Logarithmen werden auch in der Informatik verwendet, wo das binäre System allgegenwärtig ist; in der Musiktheorie, wo ein Tonhöhenverhältnis von zwei (die Oktave) allgegenwärtig ist und die Anzahl der Cents zwischen zwei beliebigen Tonhöhen dem binären Logarithmus mal 1200 ihres Verhältnisses entspricht (d. h. 100 Cents pro gleichschwebendem Halbton); und in der Fotografie zur Messung von Belichtungswerten, Lichtverhältnissen, Belichtungszeiten, Blenden und Filmempfindlichkeiten in "Blenden". ⓘ
In der folgenden Tabelle sind die gebräuchlichen Schreibweisen für Logarithmen zu diesen Basen und die Bereiche, in denen sie verwendet werden, aufgeführt. In vielen Disziplinen wird log x anstelle von logb x geschrieben, wenn die beabsichtigte Basis aus dem Kontext ersichtlich ist. Auch die Notation blog x kommt vor. In der Spalte "ISO-Notation" sind Bezeichnungen aufgeführt, die von der Internationalen Organisation für Normung (ISO 80000-2) vorgeschlagen werden. Da die Notation log x für alle drei Basen verwendet wurde (oder wenn die Basis unbestimmt oder unwesentlich ist), muss die beabsichtigte Basis oft aus dem Kontext oder der Disziplin abgeleitet werden. In der Informatik bezieht sich log in der Regel auf log2, und in der Mathematik bezieht sich log in der Regel auf loge. In anderen Kontexten bedeutet log oft log10. ⓘ
| Basis b | Bezeichnung für logb x | ISO-Schreibweise | Andere Schreibweisen | Verwendet in ⓘ |
|---|---|---|---|---|
| 2 | Binärer Logarithmus | lb x | ld x, log x, lg x, log2 x | Informatik, Informationstheorie, Bioinformatik, Musiktheorie, Fotografie |
| e | natürlicher Logarithmus | ln x | log x (in der Mathematik und vielen Programmiersprachen), loge x |
Mathematik, Physik, Chemie, Statistik, Wirtschaft, Informationstheorie und Technik |
| 10 | gewöhnlicher Logarithmus | lg x | log x, log10 x (in Technik, Biologie, Astronomie) |
verschiedene technische Bereiche (siehe Dezibel und siehe unten), Logarithmentabellen, Taschenrechner, Spektroskopie |
| b | Logarithmus zur Basis b | logb x | Mathematik |
Geschichte

Indische Mathematiker im 2. Jahrhundert v. Chr. haben als Erste Logarithmen erwähnt. Schon in der Antike nutzten sie Logarithmen zur Basis 2 für ihre Berechnungen. Im 8. Jahrhundert beschrieb der indische Mathematiker Virasena Logarithmen zur Basis 3 und 4. Ab dem 13. Jahrhundert wurden von arabischen Mathematikern ganze logarithmische Tabellenwerke erstellt. ⓘ
Nicolas Chuquet arbeitete klar die Rechengesetze für Potenzen und heraus durch eine gegenüberstellende Anordnung einer arithmetischen und einer geometrischen Reihe. ⓘ
Der deutsche Mathematiker Michael Stifel formulierte ähnlich im Jahr 1544 die Beziehungen und neben anderen Autoren des 16. Jahrhunderts. Die Reduktion von Multiplikation auf Addition steht neben trigonometrischen Additionsformeln am Beginn der Entwicklung der Logarithmen. Stifel ließ nur ganzzahlige Exponenten zu. John Napiers (1550–1617) Idee war dagegen, einen stetigen Wertebereich für die Exponenten zuzulassen. ⓘ
Im 17. Jahrhundert entwickelte der Schweizer Uhrmacher Jost Bürgi (1552–1632) ein neues System zur Berechnung von Logarithmen, das er 1620 nach langer Arbeit veröffentlichte. Aber schon vorher, im Jahre 1614, veröffentlichte der schottische Denker John Napier ein Buch über Logarithmen, das ihn als „Erfinder der Logarithmen“ berühmt machte. Ihre Arbeiten und Erkenntnisse über Logarithmen entwickelten Bürgi und Napier jedoch unabhängig voneinander. ⓘ
Das griechische Wort „Logarithmus“ bedeutet auf Deutsch „Verhältniszahl“ und stammt von Napier. Es gilt nämlich: Genau dann steht zu im selben Verhältnis wie zu (als Formel: ), wenn die Unterschiede ihrer Logarithmen übereinstimmen (als Formel: ). Erstmals veröffentlicht wurden Logarithmen von diesem unter dem Titel Mirifici logarithmorum canonis descriptio, was mit Beschreibung des wunderbaren Kanons der Logarithmen übersetzt werden kann. ⓘ
Nachdem der Oxforder Professor Henry Briggs (1561–1630) sich intensiv mit dieser Schrift beschäftigt hatte, nahm er mit ihrem Autor Kontakt auf und schlug vor, für die Logarithmen die Basis 10 zu verwenden (abgekürzt lg). Diese verbreiteten sich schnell und wurden besonders in der Astronomie geschätzt, was auch Pierre-Simon Laplace, im Vergleich zu den vorher benutzten trigonometrischen Tafeln, feststellte:
„L’invention des logarithmes, en réduisant le temps passé aux calculs de quelques mois à quelques jours, double pour ainsi dire la vie des astronomes.“ ⓘ
„Dadurch, dass die für Rechnungen benötigte Zeit von einigen Monaten auf einige Tage reduziert wurde, hat die Erfindung der Logarithmen sozusagen die Lebenszeit eines Astronomen verdoppelt.“ ⓘ
Wird die Eulersche Zahl – die im Jahre 1728 von Leonhard Euler (1707–1783) bestimmt und erstmals 1742 veröffentlicht wurde – als Basis des Logarithmus verwendet, so nennt man ihn den natürlichen Logarithmus. Der natürliche Logarithmus wird dabei durch „ln“ abgekürzt. ⓘ
Mit den Logarithmen war die mathematische Grundlage für die Weiterentwicklung des mechanischen Rechenschiebers gelegt; denn die Funktionsweise des Rechenschiebers basiert auf dem Prinzip der Addition und Subtraktion von Logarithmen. ⓘ
Die Erfindung der Funktion, die heute als natürlicher Logarithmus bekannt ist, begann mit dem Versuch von Grégoire de Saint-Vincent, einem belgischen Jesuiten, der in Prag lebte, eine Quadratur einer rechteckigen Hyperbel durchzuführen. Archimedes hatte im dritten Jahrhundert v. Chr. die Quadratur der Parabel geschrieben, aber eine Quadratur für die Hyperbel blieb bis zur Veröffentlichung der Ergebnisse durch Saint-Vincent im Jahr 1647 aus. Die Beziehung, die der Logarithmus zwischen einer geometrischen Progression in seinem Argument und einer arithmetischen Progression der Werte herstellt, veranlasste A. A. de Sarasa, die Verbindung zwischen der Quadratur von Saint-Vincent und der Tradition der Logarithmen in der Prothaphärese herzustellen, was zu dem Begriff "hyperbolischer Logarithmus" führte, einem Synonym für den natürlichen Logarithmus. Bald wurde die neue Funktion von Christiaan Huygens und James Gregory geschätzt. Die Notation Log y wurde 1675 von Leibniz übernommen, und im Jahr darauf verband er sie mit dem Integral ⓘ
Bevor Euler sein modernes Konzept der komplexen natürlichen Logarithmen entwickelte, hatte Roger Cotes ein fast gleichwertiges Ergebnis, als er 1714 zeigte, dass
- . ⓘ
Logarithmentafeln, Rechenschieber und historische Anwendungen

Durch die Vereinfachung schwieriger Berechnungen, bevor Taschenrechner und Computer zur Verfügung standen, trugen Logarithmen zum Fortschritt der Wissenschaft, insbesondere der Astronomie, bei. Sie waren entscheidend für Fortschritte in der Vermessung, der Himmelsnavigation und in anderen Bereichen. Pierre-Simon Laplace nannte Logarithmen ⓘ
- "einen bewundernswerten Kunstgriff, der, indem er die Arbeit von vielen Monaten auf einige Tage reduziert, das Leben des Astronomen verdoppelt und ihm die Fehler und den Ekel erspart, die mit langen Berechnungen verbunden sind. ⓘ
Da die Funktion f(x) = bx die Umkehrfunktion von logb x ist, wurde sie auch als Antilogarithmus bezeichnet. Heutzutage wird diese Funktion eher als Exponentialfunktion bezeichnet. ⓘ
Logarithmentafeln
Ein wichtiges Hilfsmittel, das die praktische Anwendung von Logarithmen ermöglichte, war die Logarithmentabelle. Die erste Tabelle dieser Art wurde 1617 von Henry Briggs erstellt, unmittelbar nach Napiers Erfindung, aber mit der Neuerung, 10 als Basis zu verwenden. Briggs' erste Tabelle enthielt die gemeinsamen Logarithmen aller ganzen Zahlen im Bereich von 1 bis 1000 mit einer Genauigkeit von 14 Ziffern. In der Folge wurden Tabellen mit wachsendem Umfang geschrieben. Diese Tabellen enthielten die Werte von log10 x für jede Zahl x in einem bestimmten Bereich und mit einer bestimmten Genauigkeit. Die Logarithmen zur Basis 10 wurden allgemein für Berechnungen verwendet, daher der Name gemeinsamer Logarithmus, da Zahlen, die sich durch Faktoren von 10 unterscheiden, Logarithmen haben, die sich durch ganze Zahlen unterscheiden. Der gewöhnliche Logarithmus von x lässt sich in einen ganzzahligen Teil und einen gebrochenen Teil aufteilen, der als Kennzahl und Mantisse bezeichnet wird. In Logarithmentabellen muss nur die Mantisse angegeben werden, da die Charakteristik leicht durch Zählen der Stellen hinter dem Komma bestimmt werden kann. Die Charakteristik von 10 - x ist eins plus die Charakteristik von x, und ihre Mantissen sind gleich. Unter Verwendung einer dreistelligen Logarithmentabelle wird der Logarithmus von 3542 also wie folgt angenähert ⓘ
Eine größere Genauigkeit kann durch Interpolation erreicht werden:
Der Wert von 10x kann durch Umkehrung in derselben Tabelle ermittelt werden, da der Logarithmus eine monotone Funktion ist. ⓘ
Berechnungen
Das Produkt und der Quotient zweier positiver Zahlen c und d wurden routinemäßig als Summe und Differenz ihrer Logarithmen berechnet. Das Produkt cd bzw. der Quotient c/d ergibt sich aus dem Antilogarithmus der Summe bzw. der Differenz, der in derselben Tabelle nachgeschlagen wird:
und
Bei manuellen Berechnungen, die eine nennenswerte Genauigkeit erfordern, ist das Nachschlagen der beiden Logarithmen, die Berechnung ihrer Summe oder Differenz und das Nachschlagen des Antilogarithmus viel schneller als die Multiplikation mit früheren Methoden wie der Prosthaphaeresis, die auf trigonometrischen Identitäten beruht. ⓘ
Berechnungen von Potenzen und Wurzeln beschränken sich auf Multiplikationen oder Divisionen und Nachschlagen durch
und
Trigonometrische Berechnungen wurden durch Tabellen erleichtert, die die gemeinsamen Logarithmen der trigonometrischen Funktionen enthielten. ⓘ
Rechenschieber
Eine weitere wichtige Anwendung war der Rechenschieber, ein Paar logarithmisch geteilter Skalen, die für Berechnungen verwendet wurden. Die nicht gleitende logarithmische Skala, die Guntersche Regel, wurde kurz nach der Erfindung von Napier erfunden. William Oughtred entwickelte sie weiter und schuf den Rechenschieber - ein Paar logarithmischer Skalen, die gegeneinander verschiebbar sind. Die Zahlen werden auf den verschiebbaren Skalen in Abständen platziert, die proportional zu den Differenzen zwischen ihren Logarithmen sind. Das Verschieben der oberen Skala entspricht einer mechanischen Addition von Logarithmen, wie hier dargestellt:

Addiert man zum Beispiel den Abstand von 1 zu 2 auf der unteren Skala mit dem Abstand von 1 zu 3 auf der oberen Skala, erhält man das Produkt 6, das am unteren Teil abgelesen wird. Der Rechenschieber war bis in die 1970er Jahre ein unverzichtbares Rechenwerkzeug für Ingenieure und Wissenschaftler, da er - auf Kosten der Genauigkeit - wesentlich schnellere Berechnungen ermöglicht als die auf Tabellen basierenden Verfahren. ⓘ
Analytische Eigenschaften
Ein tieferes Studium der Logarithmen erfordert den Begriff der Funktion. Eine Funktion ist eine Regel, die aus einer Zahl eine andere Zahl erzeugt. Ein Beispiel ist die Funktion, die die x-te Potenz von b aus einer beliebigen reellen Zahl x erzeugt, wobei die Basis b eine feste Zahl ist. Diese Funktion wird geschrieben als f(x) = b x. Wenn b positiv und ungleich 1 ist, zeigen wir im Folgenden, dass f invertierbar ist, wenn man es als Funktion von den reellen Zahlen zu den positiven reellen Zahlen betrachtet. ⓘ
Existenz
Sei b eine positive reelle Zahl ungleich 1 und sei f(x) = b x. ⓘ
Es ist ein Standardergebnis der reellen Analysis, dass jede stetige, streng monotone Funktion bijektiv zwischen ihrem Bereich und ihrem Gebiet ist. Diese Tatsache folgt aus dem Zwischenwertsatz. Nun ist f streng steigend (für b > 1) oder streng fallend (für 0 < b < 1), ist stetig, hat den Bereich , und hat den Bereich . Daher ist f eine Bijektion von auf . Mit anderen Worten: Für jede positive reelle Zahl y gibt es genau eine reelle Zahl x, für die gilt . ⓘ
Wir lassen den Kehrwert von f bezeichnen. Das heißt, logb y ist die einzige reelle Zahl x, für die gilt . Diese Funktion wird als Basis-b-Logarithmusfunktion oder logarithmische Funktion (oder einfach Logarithmus) bezeichnet. ⓘ
- Definitionsmenge:
- Wertemenge:
- Nullstellenmenge bzw. Kurvenschnittpunkte mit den Koordinatenachsen: {1} bzw. (1|0)
- Asymptotisches Verhalten:
Charakterisierung durch die Produktformel
Die Funktion logb x kann im Wesentlichen auch durch die Produktformel charakterisiert werden
Genauer gesagt ist der Logarithmus zu einer beliebigen Basis b > 1 die einzige steigende Funktion f von den positiven Realen zu den Realen, die f(b) = 1 erfüllt und
Graph der Logarithmusfunktion

Wie bereits erwähnt, ist die Funktion logb die Umkehrung der Exponentialfunktion . Daher entsprechen ihre Graphen einander, wenn man die x- und die y-Koordinaten austauscht (oder an der Diagonalen x = y spiegelt), wie rechts dargestellt: Ein Punkt (t, u = bt) auf dem Graphen von f ergibt einen Punkt (u, t = logb u) auf dem Graphen des Logarithmus und umgekehrt. Folglich divergiert logb (x) ins Unendliche (wird größer als eine beliebige Zahl), wenn x ins Unendliche wächst, vorausgesetzt, dass b größer als 1 ist. In diesem Fall ist logb(x) eine steigende Funktion. Für b < 1 tendiert logb (x) stattdessen gegen minus unendlich. Wenn x gegen Null geht, geht logb (x) für b > 1 gegen minus unendlich (bzw. plus unendlich für b < 1). ⓘ
Ableitung und Antiderivat

Analytische Eigenschaften von Funktionen gehen auf ihre Inversen über. Da f(x) = bx eine stetige und differenzierbare Funktion ist, gilt dies auch für logb y. Grob gesagt ist eine stetige Funktion differenzierbar, wenn ihr Graph keine scharfen "Ecken" aufweist. Da die Ableitung von f(x) durch die Eigenschaften der Exponentialfunktion zu ln(b) bx ausgewertet wird, impliziert die Kettenregel, dass die Ableitung von logb x gegeben ist durch
Das heißt, die Steigung der Tangente, die den Graphen des Basis-b-Logarithmus im Punkt (x, logb (x)) berührt, ist gleich 1/(x ln(b)). ⓘ
Die Ableitung von ln(x) ist 1/x; dies bedeutet, dass ln(x) die einzige Gegenableitung von 1/x ist, die den Wert 0 für x = 1 hat. Diese sehr einfache Formel ist der Grund dafür, den natürlichen Logarithmus als "natürlich" zu bezeichnen; dies ist auch einer der Hauptgründe für die Bedeutung der Konstante e. ⓘ
Die Ableitung mit einem verallgemeinerten funktionalen Argument f(x) ist
The quotient at the right hand side is called the logarithmic derivative of f. Computing f'(x) by means of the derivative of ln(f(x)) is known as logarithmic differentiation. The antiderivative of the natural logarithm ln(x) is:
Verwandte Formeln, wie z. B. die Antiderivate von Logarithmen nach anderen Basen, lassen sich aus dieser Gleichung mit Hilfe des Basenwechsels ableiten. ⓘ
Integrale Darstellung des natürlichen Logarithmus

Der natürliche Logarithmus von t kann als bestimmtes Integral definiert werden:
Diese Definition hat den Vorteil, dass sie sich nicht auf die Exponentialfunktion oder trigonometrische Funktionen stützt; die Definition erfolgt als Integral eines einfachen Kehrwerts. Als Integral ist ln(t) gleich der Fläche zwischen der x-Achse und dem Graphen der Funktion 1/x im Bereich von x = 1 bis x = t. Dies ergibt sich aus dem Fundamentalsatz der Infinitesimalrechnung und der Tatsache, dass die Ableitung von ln(x) gleich 1/x ist. Aus dieser Definition lassen sich Produkt- und Potenzlogarithmusformeln ableiten. Zum Beispiel wird die Produktformel ln(tu) = ln(t) + ln(u) wie folgt hergeleitet:
Die Gleichheit (1) spaltet das Integral in zwei Teile auf, während die Gleichheit (2) ein Variablenwechsel ist (w = x/t). In der folgenden Abbildung entspricht die Aufteilung der Fläche in den gelben und den blauen Teil. Wird die linke blaue Fläche vertikal um den Faktor t skaliert und horizontal um denselben Faktor verkleinert, ändert sich ihre Größe nicht. Wenn man sie entsprechend verschiebt, passt die Fläche wieder zum Graphen der Funktion f(x) = 1/x. Daher ist die linke blaue Fläche, die das Integral von f(x) von t bis tu ist, die gleiche wie das Integral von 1 bis u. Dies rechtfertigt die Gleichheit (2) mit einem eher geometrischen Beweis. ⓘ

Die Potenzformel ln(tr) = r ln(t) lässt sich auf ähnliche Weise herleiten:
Die zweite Gleichheit verwendet einen Variablenwechsel (Integration durch Substitution), w = x1/r. ⓘ
Die Summe über die Kehrwerte der natürlichen Zahlen,
wird die harmonische Reihe genannt. Sie ist eng mit dem natürlichen Logarithmus verknüpft: Wenn n gegen unendlich geht, konvergiert die Differenz,
gegen eine Zahl konvergiert (d. h. beliebig nahe kommt), die als Euler-Mascheroni-Konstante γ = 0,5772.... Diese Beziehung hilft bei der Analyse der Leistung von Algorithmen wie Quicksort. ⓘ
Transzendenz des Logarithmus
Reelle Zahlen, die nicht algebraisch sind, werden als transzendental bezeichnet; zum Beispiel sind π und e solche Zahlen, aber ist keine. Fast alle reellen Zahlen sind transzendental. Der Logarithmus ist ein Beispiel für eine transzendente Funktion. Das Gelfond-Schneider-Theorem besagt, dass Logarithmen in der Regel transzendente, d. h. "schwierige" Werte annehmen. ⓘ
Berechnung

Logarithmen sind in manchen Fällen einfach zu berechnen, z. B. log10 (1000) = 3. Im Allgemeinen können Logarithmen mit Hilfe von Potenzreihen oder dem arithmetisch-geometrischen Mittel berechnet oder aus einer vorberechneten Logarithmentabelle mit fester Genauigkeit abgerufen werden. Die Newton-Methode, ein iteratives Verfahren zur näherungsweisen Lösung von Gleichungen, kann auch zur Berechnung des Logarithmus verwendet werden, da seine Umkehrfunktion, die Exponentialfunktion, effizient berechnet werden kann. Mit Hilfe von Nachschlagetabellen können CORDIC-ähnliche Methoden verwendet werden, um Logarithmen zu berechnen, wobei nur die Operationen der Addition und Bitverschiebung verwendet werden. Darüber hinaus berechnet der binäre Logarithmus-Algorithmus lb(x) rekursiv, basierend auf wiederholten Quadrierungen von x, unter Ausnutzung der Beziehung
Potenzreihe
Taylor-Reihe
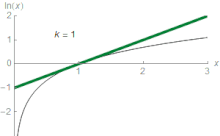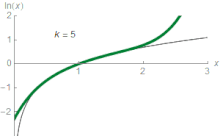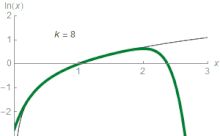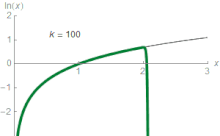
Für jede reelle Zahl z, die die Bedingungen 0 < z ≤ 2 erfüllt, gilt die folgende Formel:
Dies ist eine Kurzformel für die Aussage, dass ln(z) durch die folgenden Ausdrücke auf einen immer genaueren Wert angenähert werden kann:
Bei z = 1,5 ergibt die dritte Näherung beispielsweise 0,4167, was etwa 0,011 größer ist als ln(1,5) = 0,405465. Diese Reihe approximiert ln(z) mit beliebiger Genauigkeit, sofern die Anzahl der Summanden groß genug ist. In der Elementarrechnung ist ln(z) daher der Grenzwert dieser Reihe. Es ist die Taylorreihe des natürlichen Logarithmus bei z = 1. Die Taylor-Reihe von ln(z) liefert eine besonders nützliche Annäherung an ln(1 + z), wenn z klein ist, |z| < 1, da dann
Bei z = 0,1 ergibt die Näherung erster Ordnung beispielsweise ln(1,1) ≈ 0,1, was weniger als 5 % vom richtigen Wert 0,0953 abweicht. ⓘ
Obwohl die Folge für nur konvergiert für konvergiert, kann dies durch einen raffinierten Trick behoben werden. ⓘ
Als für alle konvergiert die Folge für denselben Bereich von z. ⓘ
Inverser hyperbolischer Tangens
Eine andere Reihe basiert auf der inversen hyperbolischen Tangensfunktion:
für eine beliebige reelle Zahl z > 0. In Sigma-Schreibweise lässt sich dies auch wie folgt darstellen
Diese Reihe kann von der obigen Taylor-Reihe abgeleitet werden. Sie konvergiert schneller als die Taylor-Reihe, insbesondere wenn z nahe bei 1 liegt. Für z = 1,5 beispielsweise approximieren die ersten drei Terme der zweiten Reihe ln(1,5) mit einem Fehler von etwa 3×10-6. Die schnelle Konvergenz für z in der Nähe von 1 kann folgendermaßen ausgenutzt werden: Bei einer Näherung mit geringer Genauigkeit y ≈ ln(z) und der Angabe
der Logarithmus von z ist:
Je besser die anfängliche Näherung y ist, desto näher liegt A bei 1, so dass sein Logarithmus effizient berechnet werden kann. A kann mit Hilfe der Exponentialreihe berechnet werden, die schnell konvergiert, sofern y nicht zu groß ist. Die Berechnung des Logarithmus von größeren z kann auf kleinere Werte von z reduziert werden, indem man z = a - 10b schreibt, so dass ln(z) = ln(a) + b - ln(10). ⓘ
Eine eng verwandte Methode kann verwendet werden, um den Logarithmus von ganzen Zahlen zu berechnen. Setzt man in die obige Reihe einsetzt, ergibt sich folgendes:
Wenn der Logarithmus einer großen ganzen Zahl n bekannt ist, dann ergibt diese Reihe eine schnell konvergierende Reihe für log(n+1) mit einer Konvergenzrate von . ⓘ
Arithmetisch-geometrische Mittelwertapproximation
Das arithmetisch-geometrische Mittel liefert hochpräzise Approximationen des natürlichen Logarithmus. Sasaki und Kanada zeigten 1982, dass dieses Verfahren besonders schnell ist, wenn die Genauigkeit zwischen 400 und 1000 Dezimalstellen liegt, während Taylor-Reihen-Methoden in der Regel schneller sind, wenn weniger Genauigkeit erforderlich ist. In ihrer Arbeit wird ln(x) durch die folgende (auf Carl Friedrich Gauß zurückgehende) Formel auf eine Genauigkeit von 2-p (oder p präzise Bits) angenähert:
M(x, y) ist das arithmetisch-geometrische Mittel von x und y. Man erhält es durch wiederholte Berechnung des Durchschnitts (x + y)/2 (arithmetisches Mittel) und (geometrisches Mittel) von x und y berechnet und diese beiden Zahlen dann zu den nächsten x und y werden lässt. Die beiden Zahlen konvergieren schnell zu einer gemeinsamen Grenze, die der Wert von M(x, y) ist. m wird so gewählt, dass ⓘ
um die erforderliche Genauigkeit zu gewährleisten. Je größer m ist, desto länger dauert die Berechnung von M(x, y) (die anfänglichen x- und y-Werte liegen weiter auseinander, so dass mehr Schritte zur Konvergenz erforderlich sind), aber desto genauer ist sie. Die Konstanten π und ln(2) können mit schnell konvergierenden Reihen berechnet werden. ⓘ
Der Feynman-Algorithmus
Während seiner Arbeit am Los Alamos National Laboratory im Rahmen des Manhattan-Projekts entwickelte Richard Feynman einen bitverarbeitenden Algorithmus zur Berechnung des Logarithmus, der der langen Division ähnelt und später in der Connection Machine verwendet wurde. Der Algorithmus nutzt die Tatsache, dass jede reelle Zahl 1 < x < 2 als ein Produkt verschiedener Faktoren der Form 1 + 2-k darstellbar ist. Der Algorithmus baut dieses Produkt P nacheinander auf, beginnend mit P = 1 und k = 1: Wenn P - (1 + 2-k) < x ist, ändert er P in P - (1 + 2-k). Dann erhöht er unabhängig davon um eins. Der Algorithmus stoppt, wenn k groß genug ist, um die gewünschte Genauigkeit zu erreichen. Da log(x) die Summe der Terme der Form log(1 + 2-k) ist, die denjenigen k entsprechen, für die der Faktor 1 + 2-k in das Produkt P aufgenommen wurde, kann log(x) durch einfache Addition berechnet werden, wobei eine Tabelle von log(1 + 2-k) für alle k verwendet werden kann. ⓘ
Anwendungen
Logarithmen haben viele Anwendungen innerhalb und außerhalb der Mathematik. Einige dieser Anwendungen stehen im Zusammenhang mit dem Begriff der Skaleninvarianz. Zum Beispiel ist jede Kammer der Schale eines Nautilus eine ungefähre Kopie der nächsten, skaliert mit einem konstanten Faktor. Daraus ergibt sich eine logarithmische Spirale. Auch das Benfordsche Gesetz über die Verteilung der führenden Ziffern lässt sich durch Skaleninvarianz erklären. Logarithmen sind auch mit Selbstähnlichkeit verbunden. So tauchen Logarithmen beispielsweise in der Analyse von Algorithmen auf, die ein Problem lösen, indem sie es in zwei ähnliche kleinere Probleme aufteilen und deren Lösungen zusammensetzen. Die Dimensionen selbstähnlicher geometrischer Formen, d. h. von Formen, deren Teile dem Gesamtbild ähneln, basieren ebenfalls auf Logarithmen. Logarithmische Skalen sind nützlich, um die relative Veränderung eines Wertes zu quantifizieren, im Gegensatz zu seiner absoluten Differenz. Da die logarithmische Funktion log(x) für große x sehr langsam wächst, werden logarithmische Skalen außerdem zur Komprimierung großer wissenschaftlicher Daten verwendet. Logarithmen kommen auch in zahlreichen wissenschaftlichen Formeln vor, z. B. in der Tsiolkowsky-Raketengleichung, der Fenske-Gleichung oder der Nernst-Gleichung. ⓘ
Logarithmische Skala

Wissenschaftliche Größen werden oft als Logarithmen anderer Größen ausgedrückt, wobei eine logarithmische Skala verwendet wird. So ist beispielsweise das Dezibel eine Maßeinheit, die mit logarithmischen Größen in Verbindung gebracht wird. Sie basiert auf dem gemeinsamen Logarithmus der Verhältnisse - dem 10-fachen des gemeinsamen Logarithmus eines Leistungsverhältnisses oder dem 20-fachen des gemeinsamen Logarithmus eines Spannungsverhältnisses. Es wird verwendet, um den Verlust von Spannungspegeln bei der Übertragung elektrischer Signale zu quantifizieren, um die Leistungspegel von Tönen in der Akustik zu beschreiben und die Absorption von Licht in den Bereichen Spektrometrie und Optik. Das Signal-Rausch-Verhältnis, das den Anteil des unerwünschten Rauschens im Verhältnis zu einem (aussagekräftigen) Signal beschreibt, wird ebenfalls in Dezibel gemessen. In ähnlicher Weise wird der Spitzenwert des Signal-Rausch-Verhältnisses üblicherweise zur Bewertung der Qualität von Ton- und Bildkompressionsverfahren unter Verwendung des Logarithmus verwendet. ⓘ
The strength of an earthquake is measured by taking the common logarithm of the energy emitted at the quake. This is used in the moment magnitude scale or the Richter magnitude scale. For example, a 5.0 earthquake releases 32 times (101.5) and a 6.0 releases 1000 times (103) the energy of a 4.0. Apparent magnitude measures the brightness of stars logarithmically. In chemistry the negative of the decimal logarithm, the decimal cologarithm, is indicated by the letter p. For instance, pH is the decimal cologarithm of the activity of hydronium ions (the form hydrogen ions H+
in Wasser). Die Aktivität von Hydronium-Ionen in neutralem Wasser beträgt 10-7 mol-L-1, daher ein pH-Wert von 7. Essig hat normalerweise einen pH-Wert von etwa 3. Die Differenz von 4 entspricht einem Verhältnis von 104 der Aktivität, d. h. die Hydronium-Ionen-Aktivität von Essig beträgt etwa 10-3 mol-L-1. ⓘ
Semilogarithmische (logarithmisch-lineare) Diagramme verwenden das Konzept der logarithmischen Skala zur Visualisierung: eine Achse, normalerweise die vertikale, ist logarithmisch skaliert. Das Diagramm rechts beispielsweise komprimiert den steilen Anstieg von 1 Million auf 1 Billion auf denselben Platz (auf der vertikalen Achse) wie den Anstieg von 1 auf 1 Million. In solchen Diagrammen erscheinen Exponentialfunktionen der Form f(x) = a - bx als Geraden mit einer Steigung gleich dem Logarithmus von b. Log-log-Diagramme skalieren beide Achsen logarithmisch, wodurch Funktionen der Form f(x) = a - xk als Geraden mit einer Steigung gleich dem Exponenten k dargestellt werden. ⓘ
Psychologie
Logarithmen kommen in mehreren Gesetzen vor, die die menschliche Wahrnehmung beschreiben: Nach dem Hick'schen Gesetz besteht ein logarithmisches Verhältnis zwischen der Zeit, die ein Mensch benötigt, um sich für eine Alternative zu entscheiden, und der Anzahl der Wahlmöglichkeiten, die er hat. Das Fitts'sche Gesetz besagt, dass die Zeit, die benötigt wird, um sich schnell zu einem Zielgebiet zu bewegen, eine logarithmische Funktion der Entfernung zum Ziel und der Größe des Ziels ist. In der Psychophysik geht das Weber-Fechner-Gesetz von einer logarithmischen Beziehung zwischen Stimulus und Empfindung aus, z. B. zwischen dem tatsächlichen und dem wahrgenommenen Gewicht eines Gegenstandes, den eine Person trägt. (Dieses "Gesetz" ist jedoch weniger realistisch als neuere Modelle wie das Stevenssche Potenzgesetz). ⓘ
Psychologische Studien haben ergeben, dass Personen mit geringer Mathematikausbildung dazu neigen, Mengen logarithmisch zu schätzen, d. h. sie positionieren eine Zahl auf einer unmarkierten Linie entsprechend ihrem Logarithmus, so dass 10 so nahe an 100 liegt wie 100 an 1000. Mit zunehmender Bildung wird dies unter bestimmten Umständen zu einer linearen Schätzung (1000 wird 10 mal so weit entfernt positioniert), während Logarithmen verwendet werden, wenn die zu zeichnenden Zahlen schwer linear zu zeichnen sind. ⓘ
Auch für die Sinnesempfindung der Helligkeit hat sich eine logarithmische Bewertung bewährt (Weber-Fechner-Gesetz), da das menschliche Auge zwischen Dämmerung und hellem Sonnenschein bis zu 10,5 Zehnerpotenzen an physikalischer Leuchtdichte überbrücken kann. ⓘ
Wahrscheinlichkeitsrechnung und Statistik

Logarithmen tauchen in der Wahrscheinlichkeitstheorie auf: Das Gesetz der großen Zahlen besagt, dass sich bei einer fairen Münze der beobachtete Anteil der Köpfe der Hälfte nähert, wenn die Anzahl der Münzwürfe ins Unendliche steigt. Die Schwankungen dieses Anteils um die Hälfte werden durch das Gesetz des iterierten Logarithmus beschrieben. ⓘ
Logarithmen kommen auch in Lognormalverteilungen vor. Wenn der Logarithmus einer Zufallsvariablen eine Normalverteilung aufweist, spricht man von einer Lognormalverteilung. Lognormalverteilungen sind in vielen Bereichen anzutreffen, wo immer eine Variable als Produkt vieler unabhängiger positiver Zufallsvariablen gebildet wird, zum Beispiel bei der Untersuchung von Turbulenzen. ⓘ
Logarithmen werden für die Maximum-Likelihood-Schätzung von parametrischen statistischen Modellen verwendet. Bei einem solchen Modell hängt die Likelihood-Funktion von mindestens einem Parameter ab, der geschätzt werden muss. Ein Maximum der Likelihood-Funktion tritt bei demselben Parameterwert auf wie ein Maximum des Logarithmus der Likelihood (der "Log-Likelihood"), da der Logarithmus eine steigende Funktion ist. Die Log-Likelihood ist einfacher zu maximieren, insbesondere bei den multiplizierten Likelihoods für unabhängige Zufallsvariablen. ⓘ
Das Benfordsche Gesetz beschreibt das Auftreten von Ziffern in vielen Datensätzen, wie z. B. der Höhe von Gebäuden. Nach dem Benford'schen Gesetz ist die Wahrscheinlichkeit, dass die erste Dezimalziffer eines Elements in der Datenstichprobe d (von 1 bis 9) ist, gleich log10 (d + 1) - log10 (d), unabhängig von der Maßeinheit. Man kann also davon ausgehen, dass etwa 30 % der Daten eine 1 als erste Ziffer haben, 18 % beginnen mit einer 2 usw. Wirtschaftsprüfer untersuchen Abweichungen vom Benford'schen Gesetz, um betrügerische Buchführung aufzudecken. ⓘ
Rechnerische Komplexität
Die Analyse von Algorithmen ist ein Zweig der Informatik, der sich mit der Leistung von Algorithmen (Computerprogrammen, die ein bestimmtes Problem lösen) beschäftigt. Logarithmen sind nützlich, um Algorithmen zu beschreiben, die ein Problem in kleinere Probleme aufteilen und die Lösungen der Teilprobleme zusammenführen. ⓘ
Um beispielsweise eine Zahl in einer sortierten Liste zu finden, prüft der binäre Suchalgorithmus den mittleren Eintrag und fährt mit der Hälfte vor oder nach dem mittleren Eintrag fort, wenn die Zahl noch nicht gefunden wurde. Dieser Algorithmus erfordert im Durchschnitt log2 (N) Vergleiche, wobei N die Länge der Liste ist. In ähnlicher Weise sortiert der Merge-Sort-Algorithmus eine unsortierte Liste, indem er die Liste in Hälften teilt und diese zuerst sortiert, bevor er die Ergebnisse zusammenführt. Merge-Sortieralgorithmen benötigen in der Regel eine Zeit, die ungefähr proportional zu N - log(N) ist. Die Basis des Logarithmus wird hier nicht angegeben, da sich das Ergebnis nur um einen konstanten Faktor ändert, wenn eine andere Basis verwendet wird. Ein konstanter Faktor wird in der Regel bei der Analyse von Algorithmen im Rahmen des Standardmodells für einheitliche Kosten vernachlässigt. ⓘ
Eine Funktion f(x) wächst logarithmisch, wenn f(x) (genau oder annähernd) proportional zum Logarithmus von x ist. (Biologische Beschreibungen des Wachstums von Organismen verwenden diesen Begriff jedoch für eine Exponentialfunktion). Zum Beispiel kann jede natürliche Zahl N in binärer Form in nicht mehr als log2 N + 1 Bits dargestellt werden. Mit anderen Worten: Der zum Speichern von N benötigte Speicherplatz wächst logarithmisch mit N. ⓘ
Entropie und Chaos

Die Entropie ist im Allgemeinen ein Maß für die Unordnung eines Systems. In der statistischen Thermodynamik ist die Entropie S eines physikalischen Systems definiert als
Die Summe bezieht sich auf alle möglichen Zustände i des betreffenden Systems, z. B. die Positionen von Gasteilchen in einem Behälter. Außerdem ist pi die Wahrscheinlichkeit, dass der Zustand i erreicht wird, und k ist die Boltzmann-Konstante. In ähnlicher Weise misst die Entropie in der Informationstheorie die Menge der Information. Wenn ein Empfänger einer Nachricht eine beliebige von N möglichen Nachrichten mit gleicher Wahrscheinlichkeit erwarten kann, dann wird die Menge an Informationen, die durch eine solche Nachricht übermittelt wird, als log2 N Bits quantifiziert. ⓘ
Lyapunov-Exponenten verwenden Logarithmen, um den Grad der Chaotizität eines dynamischen Systems zu messen. Beispielsweise führen bei einem Teilchen, das sich auf einem ovalen Billardtisch bewegt, selbst kleine Änderungen der Ausgangsbedingungen zu sehr unterschiedlichen Bahnen des Teilchens. Solche Systeme sind auf deterministische Weise chaotisch, weil kleine Messfehler des Anfangszustands vorhersehbar zu stark unterschiedlichen Endzuständen führen. Mindestens ein Lyapunov-Exponent eines deterministisch chaotischen Systems ist positiv. ⓘ
Fraktale

Logarithmen kommen in Definitionen der Dimension von Fraktalen vor. Fraktale sind geometrische Objekte, die in dem Sinne selbstähnlich sind, dass kleine Teile zumindest grob die gesamte globale Struktur reproduzieren. Das Sierpinski-Dreieck (im Bild) kann von drei Kopien seiner selbst bedeckt werden, die jeweils die Hälfte der ursprünglichen Seitenlänge haben. Damit ist die Hausdorff-Dimension dieser Struktur ln(3)/ln(2) ≈ 1,58. Eine andere logarithmusbasierte Dimension erhält man, indem man die Anzahl der Kästchen zählt, die benötigt werden, um das betreffende Fraktal abzudecken. ⓘ
Musik
Logarithmen sind mit musikalischen Tönen und Intervallen verbunden. In der gleichschwebenden Stimmung hängt das Frequenzverhältnis nur vom Intervall zwischen zwei Tönen ab, nicht von der spezifischen Frequenz oder Tonhöhe der einzelnen Töne. Zum Beispiel hat der Ton A eine Frequenz von 440 Hz und B eine Frequenz von 466 Hz. Das Intervall zwischen A und B ist ein Halbton, ebenso wie das Intervall zwischen B und B (Frequenz 493 Hz). Die Frequenzverhältnisse stimmen also überein:
Daher können Logarithmen zur Beschreibung der Intervalle verwendet werden: Ein Intervall wird in Halbtönen gemessen, indem man den Logarithmus zur Basis 21/12 des Frequenzverhältnisses nimmt, während der Logarithmus zur Basis 21/1200 des Frequenzverhältnisses das Intervall in Cents, also Hundertstel eines Halbtons, ausdrückt. Letzteres wird für eine feinere Kodierung verwendet, wie sie für nicht gleichschwebende Temperamente erforderlich ist. ⓘ
| Intervall (die beiden Töne werden zur gleichen Zeit gespielt) |
1/12 Ton |
Halbton |
Nur große Terz |
Große Terz |
Tritonus |
Oktave |
| Frequenzverhältnis r | ||||||
| Entsprechende Anzahl von Halbtönen |
||||||
| Entsprechende Anzahl von Cents |
Zahlentheorie
Natürliche Logarithmen sind eng mit dem Zählen von Primzahlen (2, 3, 5, 7, 11, ...) verbunden, einem wichtigen Thema der Zahlentheorie. Für jede ganze Zahl x wird die Menge der Primzahlen, die kleiner oder gleich x sind, mit π(x) bezeichnet. Das Primzahltheorem besagt, dass π(x) näherungsweise gegeben ist durch
in dem Sinne gegeben ist, dass das Verhältnis von π(x) und diesem Bruch sich 1 nähert, wenn x gegen unendlich tendiert. Folglich ist die Wahrscheinlichkeit, dass eine zufällig gewählte Zahl zwischen 1 und x eine Primzahl ist, umgekehrt proportional zur Anzahl der Dezimalstellen von x. Eine weitaus bessere Schätzung von π(x) ergibt sich aus der versetzten logarithmischen Integralfunktion Li(x), definiert durch
Die Riemann-Hypothese, eine der ältesten offenen mathematischen Vermutungen, kann durch den Vergleich von π(x) und Li(x) aufgestellt werden. Das Erdős-Kac-Theorem, das die Anzahl der verschiedenen Primfaktoren beschreibt, bezieht auch den natürlichen Logarithmus mit ein. ⓘ
Der Logarithmus von n faktoriell, n! = 1 - 2 - ... - n, ist gegeben durch
Daraus lässt sich die Stirling-Formel ableiten, die eine Annäherung an n! für große n darstellt. ⓘ
Verallgemeinerungen
Komplexer Logarithmus
Alle komplexen Zahlen a, die die Gleichung ⓘ
lösen, werden komplexe Logarithmen von z genannt, wenn z eine komplexe Zahl ist (als solche betrachtet wird). Eine komplexe Zahl wird im Allgemeinen als z = x + iy dargestellt, wobei x und y reelle Zahlen sind und i eine imaginäre Einheit ist, deren Quadrat -1 ist. Eine solche Zahl kann durch einen Punkt in der komplexen Ebene visualisiert werden, wie rechts dargestellt. Die Polarform kodiert eine komplexe Zahl z, die nicht Null ist, durch ihren Absolutwert, d. h. den (positiven, reellen) Abstand r zum Ursprung und einen Winkel zwischen der reellen (x-)Achse Re und der Linie, die sowohl durch den Ursprung als auch durch z verläuft. ⓘ
Der Absolutwert r von z ist gegeben durch ⓘ
Unter Verwendung der geometrischen Interpretation von Sinus und Kosinus und ihrer Periodizität in 2π kann jede komplexe Zahl z als ⓘ
für jede ganze Zahl k. Offensichtlich ist das Argument von z nicht eindeutig festgelegt: Sowohl φ als auch φ = φ + 2kπ sind gültige Argumente von z für alle ganzen Zahlen k, denn die Addition von 2kπ Bogenmaß oder k⋅360° zu φ entspricht einer "Wicklung" um den Ursprung im Gegenuhrzeigersinn um k Umdrehungen. Die resultierende komplexe Zahl ist immer z, wie rechts für k = 1 dargestellt. Man kann genau eines der möglichen Argumente von z als sogenanntes Hauptargument, Arg(z), mit einem großen A bezeichnen, indem man verlangt, dass φ zu einer bequem gewählten Windung gehört, z. B. -π < φ ≤ π oder 0 ≤ φ < 2π. Diese Bereiche, in denen das Argument von z eindeutig bestimmt ist, nennt man Zweige der Argumentfunktion. ⓘ

Die Eulersche Formel verbindet die trigonometrischen Funktionen Sinus und Kosinus mit dem komplexen Exponential:
Unter Verwendung dieser Formel und wiederum der Periodizität gelten die folgenden Identitäten:
wobei ln(r) der einzige reelle natürliche Logarithmus ist, ak die komplexen Logarithmen von z bezeichnet und k eine beliebige ganze Zahl ist. Daher sind die komplexen Logarithmen von z, d.h. all jene komplexen Werte ak, für die die ak-te Potenz von e gleich z ist, die unendlich vielen Werte ⓘ
- für beliebige ganze Zahlen k. ⓘ
Nimmt man k so, dass φ + 2kπ innerhalb des definierten Intervalls für die Hauptargumente liegt, dann heißt ak der Hauptwert des Logarithmus, bezeichnet als Log(z), wiederum mit einem großen L. Das Hauptargument jeder positiven reellen Zahl x ist 0; daher ist Log(x) eine reelle Zahl und entspricht dem reellen (natürlichen) Logarithmus. Die obigen Formeln für Logarithmen von Produkten und Potenzen lassen sich jedoch nicht auf den Hauptwert des komplexen Logarithmus verallgemeinern. ⓘ
In der Abbildung rechts ist Log(z) dargestellt, wobei die Argumente von z auf das Intervall (-π, π] beschränkt sind. Auf diese Weise weist der entsprechende Zweig des komplexen Logarithmus Unstetigkeiten entlang der negativen reellen x-Achse auf, was an dem Sprung im Farbton dort zu erkennen ist. Diese Unstetigkeit entsteht, wenn man beim Überschreiten einer Grenze auf die andere Grenze desselben Zweiges springt, d. h. nicht auf den entsprechenden k-Wert des kontinuierlich benachbarten Zweiges wechselt. Eine solche Ortskurve wird als Zweigschnitt bezeichnet. Durch den Wegfall der Bereichsgrenzen für das Argument werden die Beziehungen "Argument von z" und folglich der "Logarithmus von z" zu mehrwertigen Funktionen. ⓘ
Inversen anderer Exponentialfunktionen
Die Potenzierung kommt in vielen Bereichen der Mathematik vor, und ihre Umkehrfunktion wird oft als Logarithmus bezeichnet. So ist beispielsweise der Logarithmus einer Matrix die (mehrwertige) Umkehrfunktion der Matrixexponentialfunktion. Ein weiteres Beispiel ist der p-adische Logarithmus, die Umkehrfunktion des p-adischen Exponentials. Beide sind analog zum reellen Fall über Taylorreihen definiert. Im Zusammenhang mit der Differentialgeometrie bildet die Exponentialabbildung den Tangentenraum an einem Punkt einer Mannigfaltigkeit auf eine Nachbarschaft dieses Punktes ab. Ihre Umkehrung wird auch als logarithmische (oder log) Karte bezeichnet. ⓘ
Im Zusammenhang mit endlichen Gruppen wird die Potenzierung durch wiederholte Multiplikation eines Gruppenelements b mit sich selbst erreicht. Der diskrete Logarithmus ist die ganze Zahl n, die die folgende Gleichung löst
wobei x ein Element der Gruppe ist. Die Potenzierung kann effizient durchgeführt werden, aber der diskrete Logarithmus ist in einigen Gruppen vermutlich sehr schwer zu berechnen. Diese Asymmetrie hat wichtige Anwendungen in der Kryptographie mit öffentlichen Schlüsseln, wie z. B. im Diffie-Hellman-Schlüsselaustausch, einer Routine, die den sicheren Austausch kryptographischer Schlüssel über ungesicherte Informationskanäle ermöglicht. Der Zech'sche Logarithmus ist verwandt mit dem diskreten Logarithmus in der multiplikativen Gruppe der Nicht-Null-Elemente eines endlichen Feldes. ⓘ
Weitere logarithmusähnliche Umkehrfunktionen sind der Doppellogarithmus ln(ln(x)), der Super- oder Hyper-4-Logarithmus (eine leichte Abwandlung davon wird in der Informatik als iterierter Logarithmus bezeichnet), die Lambert-W-Funktion und der Logit. Sie sind die Umkehrfunktionen der doppelten Exponentialfunktion, der Tetration, von f(w) = wew bzw. der logistischen Funktion. ⓘ
Verwandte Konzepte
Aus der Sicht der Gruppentheorie drückt die Identität log(cd) = log(c) + log(d) einen Gruppenisomorphismus zwischen positiven reellen Zahlen unter Multiplikation und reellen Zahlen unter Addition aus. Die logarithmischen Funktionen sind die einzigen kontinuierlichen Isomorphismen zwischen diesen Gruppen. Mit Hilfe dieses Isomorphismus entspricht das Haar-Maß (Lebesgue-Maß) dx auf den Realen dem Haar-Maß dx/x auf den positiven Realen. Die nichtnegativen Realen haben nicht nur eine Multiplikation, sondern auch eine Addition und bilden einen Semiring, den so genannten Wahrscheinlichkeitssemiring; dieser ist in der Tat ein Halbfeld. Der Logarithmus macht aus der Multiplikation eine Addition (Log-Multiplikation) und aus der Addition eine Log-Addition (LogSumExp), so dass sich ein Isomorphismus von Semiringen zwischen dem Wahrscheinlichkeitssemiring und dem Log-Semiring ergibt. ⓘ
Logarithmische Einheitsformen df/f erscheinen in der komplexen Analysis und der algebraischen Geometrie als Differentialformen mit logarithmischen Polen. ⓘ
Der Polylogarithmus ist die Funktion, die durch
Er ist mit dem natürlichen Logarithmus verwandt durch Li1 (z) = -ln(1 - z). Außerdem ist Li (1) gleich der Riemannschen Zeta-Funktion ζ(s). ⓘ
Logarithmus in Anwendung und Natur
In der belebten Natur
In der belebten Natur finden sich zahlreiche Beispiele logarithmischer Spiralen, so z. B. das Wachstum von Schneckenhäusern oder die Anordnung der Kerne auf der Sonnenblume. ⓘ
Schalldruckpegel
Der Schalldruckpegel wird als logarithmisches Maß zur Beschreibung der Stärke eines Schallereignisses verwendet. Dazu wird die Hilfsmaßeinheit Dezibel (dB) verwendet. ⓘ
pH-Wert
Der pH-Wert ist das Maß für den sauren oder basischen Charakter einer wässrigen Lösung. Anmerkung: In der Chemie werden logarithmische Skalen im Allgemeinen durch ein vorangestelltes p (für Potenz) gekennzeichnet, zum Beispiel beim pKS- oder pKB-Wert. ⓘ
Richterskala
Die Richterskala, die zur Beschreibung von Erdbebenstärken genutzt wird, basiert auf einer deka-logarithmischen Einteilung. Die Erdbebenstärke steigt daher von Stufe zu Stufe exponentiell. ⓘ
Sternhelligkeiten
Sternhelligkeiten werden in astronomischen Größenklassen angegeben, die ein logarithmisches Maß der tatsächlichen Strahlungsstärke darstellt. ⓘ
Rechenschieber
Bevor elektronische Rechenmaschinen zur Verfügung standen, nutzte man die Logarithmengesetze aus, um Multiplikationen zu Additionen und Divisionen zu Subtraktionen zu vereinfachen. Die Berechnung der Quadratwurzel vereinfacht sich auf der Ebene des Logarithmus zu einer Division durch Zwei. Weil der Logarithmus selbst nicht so leicht zu berechnen ist, waren Rechenschieber mit ihren logarithmischen Skaleneinteilungen und Logarithmentafeln weit verbreitete Hilfsmittel. ⓘ
Wachstums- und Zerfallsprozesse
Typische Aufgabenstellungen bei Wachstums- und Zerfallsprozessen lassen sich durch die Umkehrfunktion des Logarithmus – die Exponentialfunktion – modellieren. Siehe Exponentieller Vorgang, Absorption. ⓘ
Anzahl der Ziffern einer Zahl
Berechnung der Anzahl der Ziffern, die zur Darstellung einer natürlichen Zahl in einem Stellenwertsystem benötigt werden. Um eine natürliche Zahl zur Basis darzustellen, werden Stellen benötigt. Die Klammern bedeuten dabei Abrunden auf die nächste ganze Zahl, die kleiner oder gleich ist. ⓘ
Zum Beispiel ist . Die obige Formel liefert den Wert 7. Man braucht also 7 Ziffern, um 100 im Dualsystem darzustellen, nämlich . Stellt man hingegen 100 im Hexadezimalsystem dar, dann benötigt man dazu zwei Stellen, denn . Es ist . ⓘ
Informationseinheit
Messung der Informationsmenge; die Informationstheorie sagt, dass, wenn etwas mit Wahrscheinlichkeit auftritt, das Wissen über das tatsächliche Auftreten davon eine Informationsmenge von bit ergibt. Zum Beispiel erhält man beim Ergebnis „Kopf“ eines fairen Münzwurfs () die Informationsmenge bit, und es genügt ein Bit, um diese Information zu codieren. ⓘ
Logarithmische Zeitskalen
Logarithmische Zeitskalen finden sich in der Geschichte der Technik ebenso wie in der geologischen Zeitskala. ⓘ
Intervalle der Musiktheorie
Intervalle haben einen exponentiellen Frequenzverlauf. Das Gehör jedoch empfindet diese als linear. Die Größen von Intervallen werden daher als multiplikative Faktoren auf Frequenzen aufgefasst und als rationale Zahlen oder als Logarithmen angegeben. In diesem Fall wird die Oktave in 1200 Cent unterteilt. Beispiel:
ⓘIntervall Frequenzverhältnis Größe 1 Oktave 2 1200 Cent 2 Oktaven 4 2400 Cent 3 Oktaven 8 3600 Cent … reine große Terz 5:4 reine Quinte 3:2
Graphische Darstellung von Funktionen
Zur graphischen Darstellung von Funktionen werden spezielle mathematische Papiere verwendet, wie beispielsweise einfachlogarithmisches Papier oder doppeltlogarithmisches Papier. ⓘ
Rechenregeln und grundlegende Eigenschaften
Logarithmengesetze
Im Folgenden wird stets vorausgesetzt, dass die Variablen von Null verschieden sind; im Falle des reellen Logarithmus werden die Zahlen sogar als positiv vorausgesetzt. Die Basen des Logarithmus dürfen ferner nicht 1 sein. ⓘ
Quotienten
Die Quotienten leiten sich direkt aus den Logarithmen von Produkten ab. Hier sei nur der einfache Fall
angegeben. Der Logarithmus eines Quotienten ist der Logarithmus des Zählers minus den Logarithmus des Nenners . ⓘ
Insbesondere ergibt sich daraus (da ):
Allgemeiner ergibt sich direkt aus der obigen Quotientenregel das Reziprozitätsgesetz:
Wurzeln
Da Wurzeln nichts anderes als Potenzen mit gebrochenem Exponenten sind, ergibt sich nach der oben angegebenen Potenzregel des Logarithmus die Rechenregel
Berechnung des Logarithmus
Die Berechnung eines Logarithmus ist prinzipiell kompliziert. Sie lässt sich „mit Papier und Bleistift“ nur durch die vielfache Wiederholung bestimmter Rechenvorgänge erreichen, wobei das Ergebnis des gerade ausgeführten Schrittes als Ausgangsbasis für den nächsten Rechenschritt verwendet wird (Iterative Vorgehensweise). Meist kann man sich dem Wert nur annähern (Approximation). Dazu gibt es verschiedene mögliche Vorgehensweisen, von denen einige im Folgenden dargestellt sind. Anfangs ist das Ergebnis dieser Teilschritte jeweils relativ weit entfernt von dem korrekten Ergebnis, wird aber bei jedem weiteren Rechenschritt genauer: es konvergiert zu dem korrekten Ergebnis. Solche iterativen Rechenoperationen sind sehr gut geeignet, um sie automatisch von einem Taschenrechner oder Computer ausführen zu lassen, wo lediglich eine Taste gedrückt werden muss (falls auf dem Gerät vorgesehen), um den Logarithmus der eingegebenen Zahl zu einer festgelegten Basis (meist der Eulerschen Zahl e = 2,718… oder der Zahl 10) zu berechnen. Die folgenden Rechenbeispiele sind jeweils nur zur Berechnung des Logarithmus einer beliebigen Zahl zur Basis e (natürlicher Logarithmus) oder 2 geeignet. ⓘ
Additive Zerlegung
Der natürliche Logarithmus steht, wie im obigen Abschnitt erwähnt, mit dem Areatangens hyperbolicus per
in Beziehung, was nach der anderen Seite aufgelöst
ergibt. ⓘ
Die Logarithmen der positiv-ganzzahligen Numeri lassen sich damit in aufsteigenden Einerstufen der Form
darstellen und ausrechnen. Dabei verbessert sich das Konvergenzverhalten der Taylorreihe
geringfügig mit wachsendem ⓘ
Mithilfe des Additionstheorems
lässt sich und damit auch additiv zerlegen. So ergeben sich beispielsweise die folgenden Identitäten für die natürlichen Logarithmen der ersten Primzahlen. Dabei werde der Übersichtlichkeit halber das Additionstheorem als Gruppengesetz
sowie seine -fache Vervielfältigung als
formuliert.
ⓘsowie
Für die praktische Rechnung sind Zerlegungen bevorzugt, deren Summanden eine Eins im Zähler haben. Wie beim Arkustangens bleiben bei der Verdoppelung
die Einsen im Zähler erhalten. ⓘ
Grenzwerte nach Hurwitz
Für den natürlichen Logarithmus gelten die Grenzwerte
sowie gleichbedeutend damit
die man leicht mit der Regel von de L’Hospital bestätigt. ⓘ
Hierauf basieren die von Adolf Hurwitz für den natürlichen Logarithmus angegebenen Grenzwerte der Folgen bzw. , die über
wobei
definiert sind. Wegen und weil monoton fallend und monoton wachsend ist, folgt die Konvergenz dieser beiden Folgen. Aufgrund von und ergibt sich die Gleichheit der beiden Grenzwerte:
Für eine praktische Berechnung von ln sind diese Grenzwerte wegen der auftretenden Auslöschung jedoch nicht gut geeignet. ⓘ
Berechnung einzelner Binärziffern
Eine weitere Möglichkeit zur Berechnung des Logarithmus besteht darin, nacheinander die Ziffern der Binärdarstellung des Logarithmus zur Basis 2 zu bestimmen. Dieses Verfahren ist besonders einfach auf Rechenwerken zu implementieren, da es aufwändige Divisionen vermeidet und auch leicht in Festkomma-Arithmetik umsetzbar ist. ⓘ
Zunächst werden die Vorkommastellen des Zweierlogarithmus (immer im Dualsystem) durch Abzählen der Vorkommastellen der Zahl bestimmt und durch Schieben auf Werte zwischen 1 und 2 normiert. ⓘ
Der Logarithmus von hat danach die Darstellung ⓘ
Quadrieren von schiebt den Logarithmus also um eine Binärstelle nach links, wodurch die Vorkommastelle möglicherweise Eins wird. Dies ist dann der Fall, wenn ist. In diesem Falle wird durch Division durch 2 wieder normiert, was keinen Einfluss auf die verbleibenden Nachkommastellen hat. Damit ergibt sich die folgende Skizze des Verfahrens:
INPUT 1 ≤ x < 2
OUTPUT Nachkommastellen bi der Binärdarstellung von log2(x) ⓘ
i ← 0
LOOP
i ← i + 1
x ← x2
IF x ≥ 2 THEN
x ← x / 2
bi ← 1
ELSE
bi ← 0
END IF
END LOOP ⓘ
Analogrechner

Zur Berechnung des Logarithmus mithilfe eines Analogrechners – also etwa der Erzeugung einer elektrischen Ausgangsspannung , die den Logarithmus des Nennwerts der Eingangsspannung annimmt – kann man sich den exponentiellen Verlauf der Strom-Spannungs-Kennlinie einer Diode zunutze machen. Die nebenstehende Skizze zeigt den prinzipiellen Aufbau eines Logarithmierers mit einem Operationsverstärker, einer Diode und einem Widerstand . ⓘ










![{\displaystyle \scriptstyle {\sqrt[{\text{degree}}]{\scriptstyle {\text{radicand}}}}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5582d567e7e7fbcdb728291770905e09beb0ea18)































![{\textstyle \log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}x}{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68ca3b6cc8ff1c0192fb0e9206d32b14aec60e02)































![{\displaystyle {\sqrt[{d}]{c}}=c^{\frac {1}{d}}=10^{{\frac {1}{d}}\log _{10}c}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cee4c3ee52a4b250c30c38836d4d58a006ce74c)




![{\displaystyle \mathbb {R} ^{+}={\mathopen {]}}0,\infty {\mathclose {[}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/468db4e96cb23e3d62fc8094c04ab400e4a445a5)


































![{\displaystyle {\frac {466}{440}}\approx {\frac {493}{466}}\approx 1.059\approx {\sqrt[{12}]{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55acf246da64ba711e1717eb43ad81792220ab32)



![{\displaystyle {\begin{aligned}2^{\frac {4}{12}}&={\sqrt[{3}]{2}}\\&\approx 1.2599\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76610ca7878ea438fa73bd50ac4df1fecce09b9f)


![{\displaystyle \log _{\sqrt[{12}]{2}}(r)=12\log _{2}(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/173477b6bc89e2396abacc83ca5015ac01b0747b)






![{\displaystyle \log _{\sqrt[{1200}]{2}}(r)=1200\log _{2}(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1ccc3b05bf5ae0d41f85c50ab1a7ceec4e95713)






































![{\displaystyle \log _{b}{\sqrt[{n}]{x}}=\log _{b}\left(x^{\frac {1}{n}}\right)={\frac {1}{n}}\log _{b}x.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67539e2acb1a493452d8ddd9912c8b2631d8b0d2)
































![{\displaystyle \ln x=\lim _{n\to \infty }n\left({\sqrt[{n}]{x}}-1\right)=\lim _{n\to \infty }n\left(1-{\frac {1}{\sqrt[{n}]{x}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7901ca277e9fe1a5be535f262d7d4a84fc51a3f)














